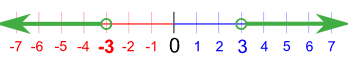代数里的绝对值
绝对值的意思是……
……一个数离零有多远:
 |
|
"6" 和零的距离是 6, 所以 6 的绝对值是 6, |
绝对值符号
要表达一个数的绝对值,使用 "|" 符号 ("直线"),像这样:
| |−5| = 5 | |7| = 7 |
 |
"|" 符号通常是在键盘的回车键(输入键)上面。 |
“官方宣言”
所以,要找绝对值,正数和零保持不变,而负数就转为正数。
写下来是这样:
x的绝对值等于:
- x,当 x 大于 零
- 0,当 x 等于 0
- −x,当 x 小于 零(把数 "倒转",变回正数)
有用的特征
以下是绝对值的一些有用特征:
|a| ≥ 0 ,永远都是!
这合理……|a|永远不能小于零。
|a| = √(a2)
a 的二次幂是正数或零(若 a是实数)。计算二次幂的平方根时把数"还原"了,但仍然保持为正数或零。
|a × b| = |a| × |b|
就是说,以下是相同的:
- (a 乘以 b)的绝对值,和
- (a 的绝对值)乘以 (b 的绝对值)。
这对解题会很有用
|u| = a 和 u = ±a 的意思是一样的
这往往是解大部分绝对值数题的关键。
例子:解 |x+2|=5
用这个特征:"|u| = a 的意思是 u = ±a":
| 这: | |x+2|=5 | |
| 和以下一样: | x+2 = ±5 |
这方程有两个答案:
| x+2 = −5 | x+2 = +5 |
| x = −7 | x = 3 |
用图来显示
为以上例子画个图:
|x+2| = 5
"=0" 的公式比较容易画图,所以每边减5:
|x+2| − 5 = 0
这是|x+2|−5的图,但为了好玩,我们用移动的方法来画这个图:
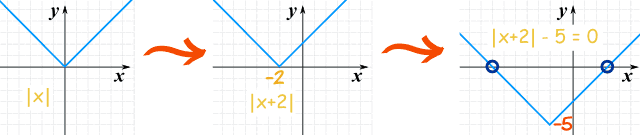 |
||
| 首先画 |x| | 然后向左移,成为 |x+2| | 再向下移,成为 |x+2|-5 |
两个解(画圈的)是−7和+3.
绝对值不等式
把绝对值和不等式掺在一起就需要小心处理了!
有4种不等式:
| < | ≤ | > | ≥ | |
|---|---|---|---|---|
| 小于 | 小于 或等于 |
大于 | 大于 或等于 |
小于、小于或等于
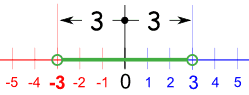
"<" 和 "≤" 会有一个以零为中心的区间:
"小于或等于"也是一样:
看看一个较为复杂的例子:
例子:解 |3x-6| ≤ 12
重写为:
−12 ≤ 3x−6 ≤ 12
加 6:
−6 ≤ 3x ≤ 18
最后,乘以(1/3)。乘以正数不会改变不等式:
−2 ≤ x ≤ 6
行了!
作为一个 区间,这可以写为: [−2, 6]
大于、大于或等于
这个有点不同……会有两个分开的区间:
小心!不要写成
−3 > x > 3 ![]()
"x" 不能同时小于 -3 和 大于 3
应该是这样:
x < −3 或 x > 3 ![]()
"x" 小于 −3 或 大于 3
"大于或等于"也是一样: