解不等式

有时候我们需要解不等式，例如：

符号	文字	例子
>	大于	x + 3 > 2
<	小于	7x < 28
≥	大于或等于	5 ≥ x - 1
≤	小于或等于	2y + 1 ≤ 7

解

我们的目标是把x（或变量的符号）独自留在不等号的左边：

像：		x < 5
或：		y ≥ 11

这样我们便 "解"了 不等式。

怎样解

解不等式和解方程非常相似……步骤大部分是相同的……

……可是我们一定要留心不等式的方向。

方向：箭头"指向"哪边

安全的运算

以下的运算对不等式的方向没有影响：

每边加（或减）一个数
每边乘以（或除以）一个正数
简化一边

但以下的运算会改变不等式的方向（例如把 "<" 变成 ">"）：

每边乘以（或除以）一个负数
左右对调

详细解释：

加或减一个值

我们时常可以在不等式的两边加（或减）一个值（像在代数入门里讲的一样）：

 

我们做了什么？

我们把这个：   变成这个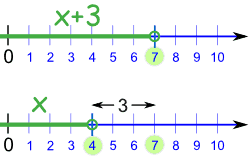：				x+3 < 7   x < 4

加 和 减很好使，因为它们对不等式没有影响

若我解了以后，"x"是在右边呢？

没关系，把不等式调换，但同时亦要把不等号倒转，以确保它仍然"指着"正确的值或项！

注意："x" 可以 在右边，但惯例是把它放在左边。

乘以或除以一个值

我们也可以把每边乘以或除以一个值（像在代数乘法里讲的一样）。

但我们要特别小心（看下去你就会知道为什么）。

正值

乘以或除以一个正数很简单，没有什么特别：

负值

当我们把不等式乘以或除以一个负数， 我们也要把不等号倒转。

看一个例子：

（注意：我在同一行做除和倒转不等号。）

所以，你只要记着：

乘以或除以变量

再来一个例子（有点刁！）：

假设你在 bx < 3b里以 1 或 -1 来代替 b：

• 若 b 是 1，答案是 x < 3
• 但若 b 是 -1，我们要解的是 -x < -3，答案便是 x > 3

答案可以使 x < 3 或 x > 3。我们不知道是哪个，因为我们不知道 b 是什么。

故此：

一个复杂的例子：

同时有两个不等式！

我们怎样同时解两个不等式？

 

总括