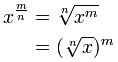分数指数
也叫"根" 或 "有理指数"
整数指数
我们首先看整数指数：
 |
一个数的指数代表把多少个这个数乘在一起。 例子：82 = 8 × 8 = 64
|
另一个例子：53 = 5 × 5 × 5 = 125
分数指数
如果指数是个分数呢？
|
指数是1/2代表平方根 指数是1/3代表立方根 指数是1/4代表四次方根 依此类推！ |
 |
为什么？
我们看一个例子来了解为什么。
首先，指数定律告诉我们在乘法里怎样处理指数：
例子：x2x2 = (xx)(xx) = xxxx = x4
就是说 x2x2 = x(2+2) = x4
我们用分数指数来试试：
例子：9½ × 9½ 是什么？
9½ × 9½ = 9(½+½) = 9(1) = 9
所以，9½ 乘以自己等于 9。
什么数乘以自己等于另一个数？ 平方根！
看：
√9 × √9 = 9
同时：
9½ × 9½ = 9
故此，9½ 和 √9 是一样的
用另一个分数来试试看
我们再来一次，不过这次指数是（1/4）：
例子：16¼
16¼ ×16¼ ×16¼ ×16¼ = 16(¼+¼+¼+¼) = 16(1) = 16
所以，4个 16¼ 相乘的结果是 16，
，故此 16¼ 是 16 的 四次方根
通用规则
从以上我们看到这规则适用于 ½ 和 ¼，其实它是通用的：
x1/n = x 的 n次方根
所以规则是：
 |
|
例子：271/3 是什么？
27 = 3
更复杂的分数呢？
若分数指数是 43/2，那怎么样？
这实际上是以任何次序做一个 立方（3）和一个 平方根（1/2）。
听我解释。
一个分数（例如 m/n）可以分拆为两部分：
- 整数部分（m），和
- 分数部分（1/n）
因为 m/n = m × (1/n)，我们可以这样做：
次序并不重要，这样 m/n = (1/n) × m 也可以：
我们的结论是：
|
|
一些例子：
例子：43/2 是什么？
43/2 = 43×(1/2) = √(43) = √(4×4×4) = √(64) = 8
或
43/2 = 4(1/2)×3 = (√4)3 = (2)3 = 8
答案一样。
例子：274/3 是什么？?
274/3 = 274×(1/3) = (274) = (531441) = 81
或
274/3 = 27(1/3)×4 = (27)4 = (3)4 = 81
第二个方法简单很多!
现在来玩玩这个图！
留心看当你在动画里改变分数时，曲线怎样畅顺地变动，显示出分数指数的精髓：
试试这些：
- 从 m=1 和 n=1 开始，然后慢慢增大 n，留心看 1/2、1/3 和 1/4
- 接着以 m=2，把 n 上下改变，留心看像 2/3 等等的分数
- 尝试把指数调成 −1
- 最后试试把 m 增大，再把 n 减少；然后 减少 m，再 增大 n：曲线会来回绕圈