指数定律

指数也叫次方

一个数的指数代表把多少个这个数乘在一起。

在这例子：8² = 8 × 8 = 64

用文字来说：8² 也可以叫 "8的2次方"、"8的2次幂" 或 "8的平方"

自己来试试：

用指数，我们可以少写很多的乘号！

例子：a⁷

a⁷ = a × a × a × a × a × a × a = aaaaaaa

留意到我们把英语字母写在一起来代表乘？在这里我们会时常这样写。

例子：x⁶ = xxxxxx

定律的重点

把所有的字母写下来对了解指数定律很重要

例子：x²x³ = (xx)(xxx) = xxxxx = x⁵

这指出 x²x³ = x⁵。等会我们会再看这个！

所以，如果你有点疑惑，把所有的字母都写下来（数目等于指数），再慢慢仔细看。

所有你需要知道的……

"指数定律"基于三个理念：

指数代表在乘法里用多少次那个数。

负指数的意思是除，因为乘的相反是除

分数指数，像 1/n 的意思是取n次方根：

若你明白这些，你就明白指数！

以下所有的定律都是基于这些理念的。

指数定律

以下为指数定律（解释在下面）：

定律	例子
x¹ = x	6¹ = 6
x⁰ = 1	7⁰ = 1
x^-1 = 1/x	4^-1 = 1/4

x^mxⁿ = x^m+n	x²x³ = x²⁺³ = x⁵
x^m/xⁿ = x^m-n	x⁶/x² = x^6-2 = x⁴
(x^m)ⁿ = x^mn	(x²)³ = x^2×3 = x⁶
(xy)ⁿ = xⁿyⁿ	(xy)³ = x³y³
(x/y)ⁿ = xⁿ/yⁿ	(x/y)² = x² / y²
x^-n = 1/xⁿ	x^-3 = 1/x³
分数指数的定律：

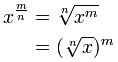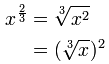定律的解释

上面头三个定律（x¹ = x, x⁰ = 1 and x^-1 = 1/x）只不过是指数序列的一部分。看：

例子：5的幂
	。。。等等。。。
5²	1 × 5 × 5	25
5¹	1 × 5	5
5⁰	1	1
5^-1	1 ÷ 5	0.2
5^-2	1 ÷ 5 ÷ 5	0.04
	。。。等等。。。

留心看列表……留意正指数、零指数和负指数都遵从同一规律，就是大5倍（或小5倍），随着指数增大（或减少）。

x^mxⁿ = x^m+n 定律

在 x^mxⁿ里，我们把多少个 "x"相乘？答案：先乘"m"次，再乘 "n"次，总共"m+n"次。

例子：x²x³ = (xx)(xxx) = xxxxx = x⁵

所以 x²x³ = x⁽²⁺³⁾ = x⁵

x^m/xⁿ = x^m-n 定律

同上，我们把几个 "x"相乘？答案："m"次，再减少"n"次（因为是除），总共是"m-n"次。

例子：x⁴/x² = (xxxx) / (xx) = xx = x²

所以， x⁴/x² = x^(4-2) = x²

（记着 x/x = 1，所以若在"线上面"有一个x，而在"线下面"也有一个x，你便可以把它们互相消除。）

这个定律也可以显示为什么 x⁰=1：

例子： x²/x² = x^2-2 = x⁰ =1

(x^m)ⁿ = x^mn 定律

先乘"m"次，然后重复"n"次，总共m×n次。

例子： (x³)⁴ = (xxx)⁴ = (xxx)(xxx)(xxx)(xxx) = xxxxxxxxxxxx = x¹²

所以 (x³)⁴ = x^3×4 = x¹²

(xy)ⁿ = xⁿyⁿ 定律

要了解这个定律，想象把所有的"x" 和 "y" 重排，如下：

例子： (xy)³ = (xy)(xy)(xy) = xyxyxy = xxxyyy = (xxx)(yyy) = x³y³

(x/y)ⁿ = xⁿ/yⁿ 定律

如上，把 "x" 和 "y" 重排

例子：(x/y)³ = (x/y)(x/y)(x/y) = (xxx)/(yyy) = x³/y³

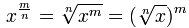定律

这个定律比较复杂！

我建议你先去分数指数看看，否则以下可能会有些混乱。

无论如何，重点是：

x^1/n = x的n次方根

所以一个分数指数，例如 4^3/2，的意思是以任何次序去取一个立方（3）和一个平方根（1/2）。

记着分数 m/n = m × (1/n)：

例子：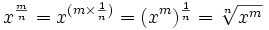

次序不重要，所以这样 m/n = (1/n) × m 也可以:

例子：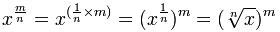

好了，就这么多！

如果你觉得要记着这么多个定律很困难，不要忘记：

只要你记着及了解
上面的三个理念，你随时可以动动脑筋，自己把定律导出来。

最后，还有一个重要的细节……如果 x= 0 呢？

正指数（n>0）		0ⁿ = 0
负指数（n<0）		未定义！（因为除以 0 是未定义的）
指数 = 0		嗯……看下面！

奇怪的 0⁰

0⁰是什么？有两个说法。

0⁰ 可以是 1，或 0，所以有些人说它是"不确定的"：

	x⁰ = 1，所以。。。	0⁰ = 1
	0ⁿ = 0，所以。。。	0⁰ = 0
	有疑问……	0⁰ = "不确定"

难题：

指数定律

例子：a7

例子：x6 = xxxxxx

定律的重点

例子：x2x3 = (xx)(xxx) = xxxxx = x5

所有你需要知道的……

指数定律

定律的解释

xmxn = xm+n 定律

例子：x2x3 = (xx)(xxx) = xxxxx = x5

xm/xn = xm-n 定律

例子：x4/x2 = (xxxx) / (xx) = xx = x2

例子： x2/x2 = x2-2 = x0 =1

(xm)n = xmn 定律

例子： (x3)4 = (xxx)4 = (xxx)(xxx)(xxx)(xxx) = xxxxxxxxxxxx = x12

(xy)n = xnyn 定律

例子： (xy)3 = (xy)(xy)(xy) = xyxyxy = xxxyyy = (xxx)(yyy) = x3y3

(x/y)n = xn/yn 定律

例子：(x/y)3 = (x/y)(x/y)(x/y) = (xxx)/(yyy) = x3/y3

定律

例子：

例子：

好了，就这么多！

最后，还有一个重要的细节……如果 x= 0 呢？

奇怪的 00

例子：a⁷

例子：x⁶ = xxxxxx

例子：x²x³ = (xx)(xxx) = xxxxx = x⁵

x^mxⁿ = x^m+n 定律

例子：x²x³ = (xx)(xxx) = xxxxx = x⁵

x^m/xⁿ = x^m-n 定律

例子：x⁴/x² = (xxxx) / (xx) = xx = x²

例子： x²/x² = x^2-2 = x⁰ =1

(x^m)ⁿ = x^mn 定律

例子： (x³)⁴ = (xxx)⁴ = (xxx)(xxx)(xxx)(xxx) = xxxxxxxxxxxx = x¹²

(xy)ⁿ = xⁿyⁿ 定律

例子： (xy)³ = (xy)(xy)(xy) = xyxyxy = xxxyyy = (xxx)(yyy) = x³y³

(x/y)ⁿ = xⁿ/yⁿ 定律

例子：(x/y)³ = (x/y)(x/y)(x/y) = (xxx)/(yyy) = x³/y³

奇怪的 0⁰