多项式:零点的上下界
一个巧妙的方法来告诉你在哪里寻找多项式的根。
多项式看起来像这样:
| 多项式例子 这个多项式有 3 项 |
多项式有系数:
项是从大至小的指数排列
(在技术层面,7 是个常数,但在这里全部视为系数是比较容易的。)
多项式也有根:
"根"(或"零点")是多项式等于零的地方。
例子:当 x=2时,3x - 6 等于 零 ,因为 3(2)-6 = 6-6 = 0
根(零点)在哪里?
有时要寻找根的位置是很困难的!
……在哪里找……向左和向右找多远?
有一个巧妙的方法去决定在哪里可以找到所有的实数根。
只需要简单的算术!
步骤
首先,整理数据!
- 首项系数一定要是 1。如果不是,把所有的项除以第一项的系数。
- 写下所有的系数。
- 拿走首项系数!
- 拿走负号。
- 我们只用剩下的值来继续做下去
接下来我们用这些值来计算两个"界限":
- 界限 1:把最大值加 1。
- 界限 2:选比较大的:1,或 所有值的和。
小的"界限"便是答案……
……所有根都是在这个界限的正值(上界)与负值(下界)之间!
例子
例子:x3 + 2x2 - 5x + 1
首项系数是 1,所以我们可以去下一步。
系数是:1、2、-5、1
拿走首项系数和负号:2、5、1
- 界限 1:最大值是 5。加 1 = 6
- 界限 2:所有值的和是:2+5+1 = 8
小的界限是 6
所有的实数根是在 -6 与 +6 之间
故此,我们只需绘画从 -6 到 6 的图来找实数根。但是最好多画一点,好使我们可以看到任何正好在 -6 或 6 的根:
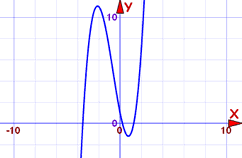
我们现在可以扩大画面来看到较为准确的值
例子:10x5 + 2x3 - x2 - 3
首项系数是 10,所以我们把全部的项除以 10:
x5 + 0.2x3 - 0.1x2 - 0.3
系数是:1、0.2、-0.1、-0.3
拿走首项系数和负号:0.2、0.1、0.3
- 界限 1:最大值是 0.3。加 1 = 1.3
- 界限 2:所有值的和是:0.2+0.1+0.3 = 0.6。这是小于 1,所以答案是 1
小的界限是 1.
所有实数根是在 -1 与 +1 之间
现在你自己来画图。
附注
上面的 "界限 1" 和 "界限 2" 并不是唯一寻找多项式的根的上下界的方法,但它是最容易的方法!