正弦定理
正弦定理(或称正弦定律)对解三角形非常有用:
a sin A = b sin B = c sin C
它适用于任何三角形:
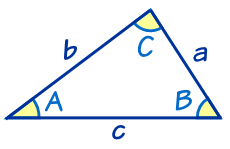 |
a、b 和 c 是边。 A、B 和 C 是角。 (边 a 对着 角 A、 |
定理说:
边 a 的长度 除以 角 A 的正弦
等于 边 b 的长度 除以 角 B 的正弦,
也等于 边 c 的长度 除以 角 C 的正弦
?????
好,我们用一个三角形来计算一下:
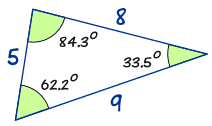 |
a sin A = 8 sin(62.2°) = 8 0.885…… = 9.04…… b sin B = 5 sin(33.5°) = 5 0.552…… = 9.06…… c sin C = 9 sin(84.3°) = 9 0.995…… = 9.05…… |
答案都差不多是相同的!
(若我们的计算有完全的准确度,答案便会是完全相同的)。
你可以看到:
a sin A = b sin B = c sin C
有什么用?
举个例看看:
例子:求 边 "c" 的 长度
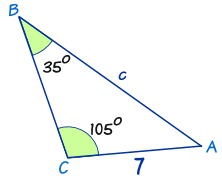
| 正弦定理 | a/sin A = b/sin B = c/sin C | |
| 代入已知值: | a/sin A = 7/sin(35°) = c/sin(105°) | |
| 拿走 a/sin A (在这里没用): | 7/sin(35°) = c/sin(105°) | |
| 用代数来重排及解: | ||
| 换边: | c/sin(105°) = 7/sin(35°) | |
| 每边乘以 sin(105°): | c = ( 7 / sin(35°) ) × sin(105°) | |
| 计算: | c = ( 7 / 0.574…… ) × 0.966…… | |
| 计算: | c = 11.8 (保留一个小数位) | |
求未知角度
在上面的例子,我们求未知边长……
……但我们也可以用正弦定理来求未知角度。
求角度时,最好把分数倒转(把 a/sin A 变成 sin A/a,等等):
sin A a = sin B b = sin C c
例子:求 角 B
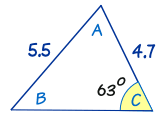
| 开始: | sin A / a = sin B / b = sin C / c | |
| 代入已知值: | sin A / a = sin B / 4.7 = sin(63°) / 5.5 | |
| 拿走 "sin A / a": | sin B / 4.7 = sin(63°) / 5.5 | |
| 每边乘以 4.7: | sin B = (sin(63°)/5.5) × 4.7 | |
| 计算: | sin B = 0.7614…… | |
| 反正弦: | B = sin-1(0.7614……) | |
| B = 49.6° |
有时会有两个答案!
我们要注意一个微妙的细节:
可能有两个答案。
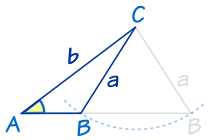 |
假设我们知道 角 A 和 边 a 与 b。 我们可以把边 a 放在左边或右边(如图),从而得到两个结果(一个小三角形和一个大三角形) 两个答案都是对的! |
这只会在 "两边和非 夹角" 的情形发生,亦不会一定发生,但我们仍然需要留意。
想: "我可以把那条边放到另一边来得到另一个正确的答案吗?"
例子:求 角 R
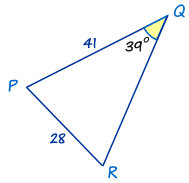
这三角形用不同的标志:PQR 而不是 ABC。没关系,就在正弦定理用 P、Q 和 R 就行了。
| 开始: | sin R / r = sin Q / q | |
| 代入已知值: | sin R / 41 = sin(39°)/28 | |
| 每边乘以 41: | sin R = (sin(39°)/28) × 41 | |
| 计算: | sin R = 0.9215…… | |
| 反正弦: | R = sin-1(0.9215……) | |
| R = 67.1° |
慢着!还有另外一个角的正弦是等于 0.9215…… 的!
计算器不会给你这个答案,但 sin(112.9°) 也是等于 0.9215……
那么,我们怎样得到 112.9°这个答案?
其实很简单……把 67.1°从 180°减去,像这样:
180° - 67.1° = 112.9°
故此,R 可以有两个答案: 67.1°和 112.9°:
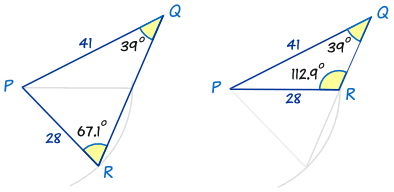
两个都是对的!每个三角形都有 39°的角及 41 和 28 长的边。
所以,一定要记得去检查,看看可不可以有另一个答案。
- ……有时候会有两个答案(如上)
- ……有时候只有一个答案(如下)
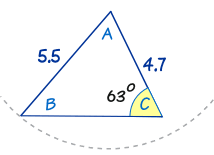 |
我们以前也看过这个三角形。 你可以尝试把 "5.5" 长的边放到右边,但这样不会形成一个符合给定条件的三角形,所以也不会导致一个合理的答案。 故此,这算题只有一个答案。 |