余弦定理
余弦定理对解三角形是非常有用的:
![]()
这定理适用于任何三角形:
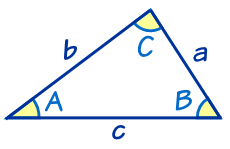 |
a、b 和 c 是三角形的边。 C 边 c 的对角 |
我们举个例来看看:
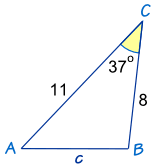
例子:"c" 的长度是多少?
已知: C = 37º、a = 8 和 b = 11
| 余弦定理说: | c2 = a2 + b2 − 2ab cos(C) | |
| 代入已知值: | c2 = 82 + 112 − 2 × 8 × 11 × cos(37º) | |
| 计算: | c2 = 64 + 121 − 176 × 0.798… | |
| 计算: | c2 = 44.44... | |
| 开平方: | c = √44.44 = 6.67 保留两位小数 |
答案:c = 6.67
怎样记
怎样去记这公式呢?
公式其实是在 勾股定理 上多加一点,使其适用于所有的三角形:
| 勾股定理: | a2 + b2 = c2 | (只适用于直角三角形) | ||
| 余弦定理: | a2 + b2 − 2ab cos(C) = c2 | (适用于所有三角形) |
这样记:
- 想英语字母 "abc":a2 + b2 = c2,
- 再来一个 "abc": 2ab cos(C),
- 放在一起:a2 + b2 − 2ab cos(C) = c2
什么时候用
在以下的情形,我们可以用余弦定理:
- 已知三角形的两边和两边中间的夹角,求第三边(像上面的例子)
- 已知三角形的三边,求其角度(如以下的例子)
例子:角 "C" 是多大?
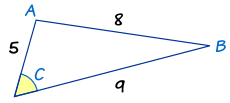
长度为 "8" 的边的对角是 C,所以这边是 c。另外两条边是 a 和 b。
把已知值代入余弦定理::
| 开始: | c2 = a2 + b2 − 2ab cos(C) | |
| 代入 a、b 和 c: | 82 = 92 + 52 − 2 × 9 × 5 × cos(C) | |
| Calculate: | 64 = 81 + 25 − 90 × cos(C) | |
| 重排及解: | ||
| 每边减 25: | 39 = 81 − 90 × cos(C) | |
| 每边减 81: | −42 = −90 × cos(C) | |
| 两边对调: | −90 × cos(C) = −42 | |
| 除以 −90: | cos(C) = 42/90 | |
| 取逆余弦: | C = cos-1(42/90) | |
| 用计算器: | C = 62.2° (保留一位小数) | |
其他形式
求角度的简易形式
上面我们看到已知三边是怎样去求角度。我们用了几步来做,但其实用 "直接" 公式会比较简单(公式只不过是重排这公式: c2 = a2 + b2 − 2ab cos(C) )。公式可以有三个形式:
cos(C) = a2 + b2 − c2 2ab
cos(A) = b2 + c2 − a2 2bc
cos(B) = c2 + a2 − b2 2ca
例子:用余弦定理(角度形式)来求角 "C"
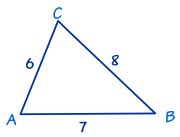
已知三边:
- a = 8,
- b = 6 和
- c = 7。
用余弦定理(角度形式)来求角 C:
| cos C | = (a2 + b2 − c2)/2ab |
| = (82 + 62 − 72)/2×8×6 | |
| = (64 + 36 − 49)/96 | |
| = 51/96 | |
| = 0.53125 | |
| C | = cos-1(0.53125) |
| = 57.9° 保留一位小数 |
a、b 和 c 的形式
你也可以重写 c2 = a2 + b2 - 2ab cos(C) 公式为 "a2=" and "b2=" 的形式。
以下是这三个形式:
![]()
![]()
![]()
但最容易是记着 "c2=" 的形式,然后在应用时用不同的字母!
如下:
例子:求长度 "z"
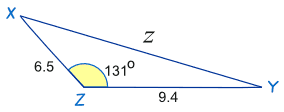
字母不同!没关系。我们可以以 x 代替 a、y 代替 b 和 z 代替 c
| 开始: | c2 = a2 + b2 − 2ab cos(C) | |
| x 代替 a、y 代替 b 和 z 代替 c | z2 = x2 + y2 − 2xy cos(Z) | |
| 代入已知值: | z2 = 9.42 + 6.52 − 2×9.4×6.5×cos(131º) | |
| 计算: | z2 = 88.36 + 42.25 − 122.2 × (−0.656...) | |
| z2 = 130.61 + 80.17…… | ||
| z2 = 210.78…… | ||
| z = √210.78…… = 14.5 保留一位小数。 |
答案:z = 14.5
留意到 cos(131º) 是负数吗?这把最后的正负号变成 +(正)号了。钝角的余弦一定是负数(见 单位圆)。