解 SSA 三角形
"SSA" 的意思是 "(S)ide, (S)ide, (A)ngle"(英语 "Angle" 的意思是 角,"Side" 的意思是 边)
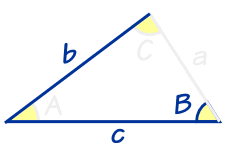 |
"SSA" 的意思是我们知道两个边长和一个角度,(而这个角不是 在已知的两条边之间)。 |
解 SSA 三角形
|
例 1
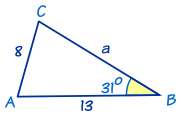
在这三角形,我们知道:
- 边 b = 8
- 边 c = 13
我们可以用 正弦定理 来求角 C:
接着用 三角形三个内角的和是 180° 来求角 A:
现在用正弦定理来求 a:
注意:我们没有用 A = 92.2°,因为这数只是准确到一个小数位,所以用上一步得到的 92.181……°会准确很多。计算器里应该还保留了这个数。
三角形解了 ……
…… 真的解了?
* 在上面计算:
C = sin−1(0.8369……)
C
= 56.818……°
我们没想到 sin−1(0.8369……) 会有两个答案(看 正弦定理)
C 的另外一个答案是 180° − 56.818……°
在这里你可以看到为什么可能会有两个答案:
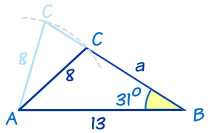
把 "8" 长的边放在左边或右边便可能
与边 "a" 在两个可能的地方接触。
例子(续):
另外一个答案是:
C 的值不同,角 A 和 边 a的值也不同
用 "三角形三个内角的和是 180°" 来求 角 A:
现在可以用正弦定理来求 a:
所以两组答案是:
C = 56.8°、A = 92.2°、a = 15.52
C = 123.2°、A = 25.8°、a = 6.76
例 2
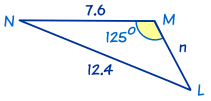
这也是个 SSA 三角形。
在这三角形,我们知道角 M = 125°、m = 12.4 和 l = 7.6
我们先用正弦定理来求角 L:
接着我们用 "三角形三个内角的和是 180°" 来求 角 N:
现在再用正弦定理来求 n:
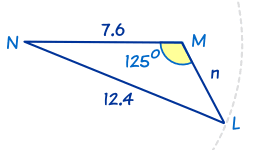
注意:这例子只有一个答案。"12.4" 长的边只在一个地方和另外的边接触。
L 的另外一个可能答案是 149.9°。但在这例子这是不可能的,因为已经有 M = 125°,而一个三角形不可以有两个角大于 90°。
结论:
解 "Side, Side, Angle"(SSA)三角形时,我们需要
检查有没有另外一个答案!