二进制、十进制和十六进制数
十进制数
要理解二进制数和十六进制数,最好是先去理解十进制数。
在一个十制进数里,每个数字都有一个“位置”,而小数点告诉我们每个位置是什么。
小数点左边是“单位”的位置。向左过去,每一个位置大10倍,而向右每一个位置小10倍:
这只是其中一个记录数值的方式。其他方式包括罗马数字,二进制,十六进制,等等。你甚至可以在纸上画点来表示数值!
十进制数系统也被称为“以10为底的数”,因为它是基于10 这数字。
它有10个符号(0、1、2、3、4、5、6、7、8 和 9),但有趣的是:没有“十”的符号。“10”,实际上是两个符号放在一起,一个“1”和一个“0”:
在十进制,你这样数:“0、1、2、3、4、5、6、7、8、9、……”,然后你再没有符号了!
所以,你在左边加个 1,然后从 0 重新开始: 10、11、12、……
用不同数字系统计数
你不一定要用10作为“底”。你可以用2(“二进制”),16(“十六进制”)、或者任何你想用的数字!
例如:在二进制,你这样数:“0、1、……”,然后你再没有符号了!
所以,你在左边加个 1,然后从 0 重新开始:10,11 ……
看看这个示例,去了解如何在以 2为底 到以 16为底 的数字系统里 计算点数:
| 试试这个:选择一个底,看它数一会儿,然后按“||”(暂停)。再看看数出来的点的数目对不对,像这个用 2 为底的例子: | 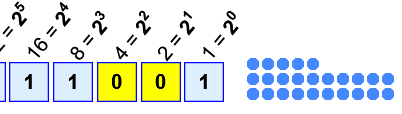 |
| 例子: | 1×16 + 1×8 + 1×1 = 16 + 8 + 1 = 25 |
所以,原则是:
数到比“底”少一,然后从 0 重新开始,但是先把左边的数字加 1。
二进制数
二进制数的不同不过是用“2 为底”,而不是用 10。你从 0 开始数,数到1,就没有数字了……所以你从 0 重新开始,但把左边的数字加 1。
像这样:
000 |
||
001 |
||
010 |
二进制里没有“2”,所以从 0 重新开始…… ...把左边的数字加 1 |
|
011 |
||
100 |
再重新从 0 开始,并加 1 到左边的数字…… ……但该数字已经是 1,所以它也返回到 0 ...…… ……并把 1 加到下一个左边的数字上 |
|
101 |
||
110 |
依此类推…… |
十六进制数
十六进制数系统很有趣,它有16个符号!
从 1 到 9,它们和十进制数字一样,但随后用英语字母(“A”、“B”、“C”、“D”、“E”、“F”)来代替十进制数 10 到 15。
所以,一个十六进制数字可以显示16个不同的值,而不是通常的10个:
| 十进制: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 十六进制: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
