换元积分法
"换元积分法" 是求积分的方法,适用于可以写成一个特定格式的函数。
第一步,也是最重要的一步,是把积分写成这个格式:

注意积分里有 g(x) 和它的 导数 g'(x)
像这例子:
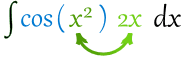
在这例子里,f=cos,g=x2,还有其导数 2x
格式对了,可以用换元积分法来求这个积分了!
若积分写成了这个格式,我们可以做这个变换(换元):
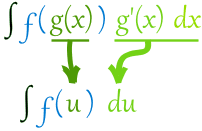
接着我们可以求 f(u) 的积分,然后把 g(x) 代回去 u 里。
像这样:
例子:∫cos(x2) 2x dx
这已经是可以换元的格式:
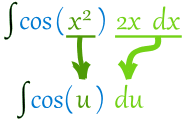
求积分:
∫cos(u) du = sin(u) + C
把 u=x2 代回去:
sin(x2) + C
所以∫cos(x2) 2x dx = sin(x2) + C。 不错!(当然不错,不然我不会举这个例了!)
换元积分法只适用于某些积分,并且可能需要先重排式子:
例子:∫cos(x2) 6x dx
糟了!是 6x,不是 2x。格式不对了!
没关系。重排积分就行了:
∫cos(x2) 6x dx = 3∫cos(x2) 2x dx
(常数乘数可以移到外面。见 积分法则。)
可以照样做了:
3∫cos(u) du = 3 sin(u) + C
把 u=x2 代回去:
3 sin(x2) + C
做好了!
我们来看一个比较复杂的例子::
例子:∫x/(x2+1) dx
好…… x2+1 的导数是 2x …… 所以我们可以这样重排:
∫x/(x2+1) dx = ½∫2x/(x2+1) dx
得到:
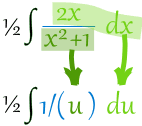
求积分:
½∫1/u du = ½ ln(u) + C
把 u=x2+1 代回去:
½ ln(x2+1) + C
来看看这个:
例子:∫(x+1)3 dx
…… x+1 的导数是 …… 1!
所以:
∫(x+1)3 dx = ∫(x+1)3 · 1 dx
得到:
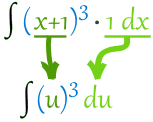
求积分:
∫u3 du = (u4)/4 + C
把 u=x+1 代回去:
(x+1)4 /4 + C
就是这样!
总结
若积分可以写成这个格式:

我们便可以做这个变换:u=g(x),然后求积分∫f(u) du
最后把 g(x) 代回 u 里。