积分入门

积分是把片相加来求整体。

积分可以用来求面积、体积、中点和很多其他有用的东西。要了解积分，最简单是从求 函数曲线下面的面积开始。像这样：

积分面积
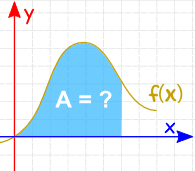
y = f(x) 下面的面积是多少？

片

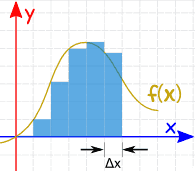
我们可以求函数在几点的值，然后把宽度为Δx的片的面积加起来（但答案不会很精确）：

   积分面积大deltax
     

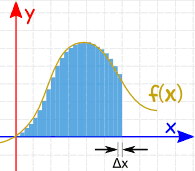
我们可以使 Δx 非常小，然后 把很多片的面积加起来（答案比上面的好一点）：

 

   积分面积小deltax
     

当片的 宽度趋近零时，答案也趋近正确的面积。

我们用 dx 来代表趋近零的宽度 Δx。

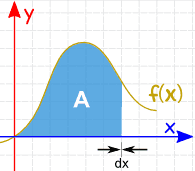   积分面积 dx

有很多块片要相加！

可是，我们不需要做加法，有个 "捷径"。因为……

…… 求积分与求导数是相反的。

（所以你需要先了解 导数！）

如下：

例子：2x 的积分是什么？

积分与导数

 

我们知道 x2 的导数是 2x ……

 

…… 所以 2x 的积分是 x2

下面有更多例子。

记法

"积分" 的符号像英语字母 "S"
（源自英语 "Sum"（总和））：

   integral notation

把要求积分的函数（叫被积函数）放在积分符号后面，

最后放 dx 来代表积分的方向是 x（片沿 x 的宽度趋近零）。

我们这样写答案：

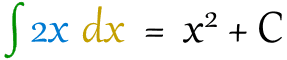
2x dx = x^2 + C 的积分

加 C

答案我们已经写了 x2，但为什么要加个 + C？

这个叫 "积分常数"。我们需要把它写上，因为有很多函数的导数都是 2x：

很多积分与一个导数

x2+4 的导数是 2x，x2+99 的导数也是 2x，…… ！因为常数的导数是零。

当我们把计算 倒转 来求积分时，我们只知道 2x，但其实答案可以有任何一个常数。

所以我们需要在答案后面加上 + C。

 

水龙头和水箱

积分水龙头和水箱

积分就像用水龙头向水箱注水。

输入（积分前）是龙头的流速。

把水流积分（把水流一小点一小点地加起来）的结果是水箱里的水的体积。

 

想象流速从 0 开始，逐渐增大（可能有个机器控制着水龙头）。

积分水龙头和水箱图

刘率越来越大，注水也越来越快。

如果流速是 2x，水箱注满的速度是 x2。

我们把流速积分可以得到体积。

例子：3 分钟后（x=3）（假设流速的单位是升每分钟）：

 

我们也可以反过来做：

积分水龙头和水箱图

想象你不知道流速。
你只知道体积以 x2 的速度增加。

我们可以反过来做（用导数来求坡度），而得到流速为 2x。

例子：2 分钟后，体积的坡度是 4，意思是它以每分种 4 升的速度增大（=流速）。同样，在 3 分钟时，坡度是 6，等等。

积分与导数  

所以积分和导数是相反的。

我们可以这样写下来：

流速 2x 的积分是水的体积：

   ∫2x dx = x2 + C

体积增大的坡度 x2+C 是流速：

   d/dx(x2 + C) = 2x

 

积分水龙头和水箱图

这例子也可以解释上面讲的常数 "C"……可能水箱里本来已经有一点水！

所以我们一定需要加上 "+ C"。

其他函数

详细分析 y=2x 后，我们现在来看看其他函数。

如果我们已经知道函数是另一个函数的导数，我们便已知道答案（因为积分和导数是相反的）。可是……不要忘了加 C。

例子：∫cos(x) dx 是什么？

积分与倒数，cos(x) vs sin(x)

在 导数法则表 里，sin(x) 的导数是 cos(x)，所以：

∫cos(x) dx = sin(x) + C

其实很多这种 "倒转" 都已经做好了（去看 积分法则）。

例子：∫x3 dx 是什么？

在 积分法则 的 "幂次方法则" 说明：

∫xn dx = xn+1/(n+1) + C

用这个法则，设 n=3：

∫x3 dx = x4 /4 + C

懂得合适需要用积分法则是熟悉积分运算的重点.

所以……好好学习积分法则，并且做很多练习。

学好积分法则。练习！ 练习！ 练习！
（下面有练习题）

定积分与不定积分

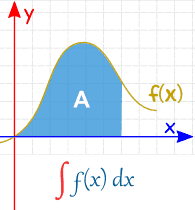
我们上面做的都是不定积分。

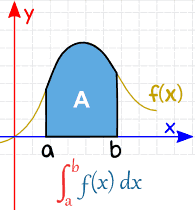
定积分 有下限和上限的值（写在 "S" 符号的下面和上面）：

不定积分   定积分
不定积分   定积分

去看看 定积分 来了解更多。

 

 
积分法则 微积分索引