定积分
你也许想先阅读 积分入门!
积分
积分 可以用来求面积、体积、中点和很多其他有用的东西。我们时常用积分来求函数曲线下面的面积。像这样: |
 |
|
我们可以把曲线下面的面积切成一片片,当这些片的宽度趋近零时,它们面积的和便是曲线下面的面积: 也有 积分法则 来帮我们求答案。 |
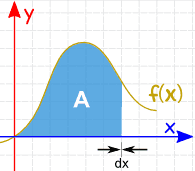 |
记法
"积分" 的符号像英语字母 "S" |
把要求积分的函数(叫被积函数)放在积分符号后面,
最后放 dx 来代表积分的方向是 x(片沿 x 的宽度趋近零)。
定积分
定积分 有起点和终点:有从 a 到 b 的区间。
起点和终点的值放在"S" 符号的下面和上面,像这样:
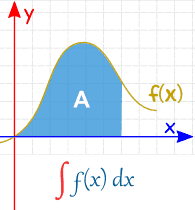 |
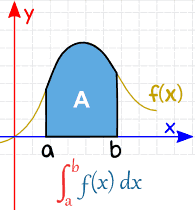 |
|
| 不定积分 (没有指定值) |
定积分 (从 a 到 b) |
定积分是不定积分在 a 和 b 的值的差:
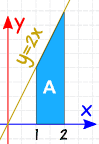
例子:
2x dx 从 1 到 2 的定积分:
![]()
不定积分 是:∫2x dx = x2 + C
- 在 x=1:∫2x dx = 12 + C
- 在 x=2:∫2x dx = 22 + C
减:
"C" 被消去…… 所以求定积分时我们可以不理 C。
答案可以直接写为:
![]()
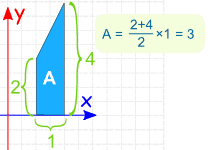
我们可以求那个图形(梯形)的面积来检验答案:
对了,面积是 3.
(不赖!)
再看一个例子:
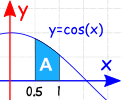
例子:
cos(x) dx 从 0.5 到 1.0 的定积分:
![]()
(注意:x 的单位一定要是 弧度)
不定积分是:∫cos(x) dx = sin(x) + C
C 可以不理(如上):
| = sin(1) − sin(0.5) | ||
| = 0.841…… − 0.479…… | ||
| = 0.362…… |
现在我们用以下的例子来表明一个论点:
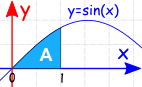
例子:
sin(x) dx 从 0 到 1 的定积分:
![]()
不定积分是:∫sin(x) dx = −cos(x) + C
起点是 0,那么我们可不可以求 x=1 的值为面积?
−cos(1) = −0.540……
什么?在 x=1 的面积是负数?不,我们一定要减去积分在 x=0 的值,我们不可以假设它是零。
正确的做法是求两个值的差(C 会消去,所以不用写下来):
| = −cos(1) − (−cos(0)) | ||
| = −0.540……− (−1) | ||
| = 0.460…… |
像样多了!
但若曲线是在轴的下面,便真的可以有负的面积:
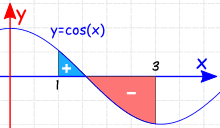
例子:
cos(x) dx 从 1 到 3 的定积分:
![]()
注意曲线有正的部分,也有负的部分。
定积分是净面积的值。
不定积分是:∫cos(x) dx = sin(x) + C
计算:
| = sin(3) − sin(1) | ||
| = 0.141…… − 0.841…… | ||
| = −0.700…… |
试试用不同的起点和终点来求 cos(x) 的定积分,来更加了解有正值和负值的函数的定积分。
可是,有时我们需要 实际面积 (不减去负的部分):
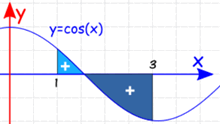
例子:从 x = 1 到 x = 3,y = cos(x) 和 x轴 之间的面积是多少?
这和上面的例子差不多,不过面积是个正数 (想象你需要为它涂色)。
我们要把两个部分分开来做:
- 一部分是 x轴 上面的面积
- 一部分是 x轴 下面的面积
曲线在 x = π/2 经过 x轴,所以:
最后一个是负值,但我们要正值,所以:
总面积 = 0.159…… + 0.859…… = 1.018……
答案和上面的例子相差很大。
连续
求积分的函数在 a 和 b 之间一定要是 连续 的:没有缺口、间隙或垂直渐近线(函数向上或下趋向无穷大)。
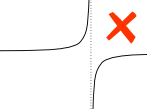
例子:
在 a 和 b 之间的垂直渐近线对定积分有影响。
属性
倒转区间
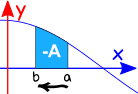
把区间倒转后,定积分是原来定积分的负值。
![]()
零长度的区间
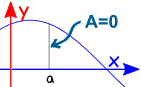
若起点等于终点,定积分的值是零:
![]()
区间相加
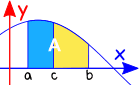
我们也可以把两个区间的定积分相加:
![]()
总结
从 a 到 b 的定积分是用在 b 的不定积分减去在 a 的不定积分。