椭圆的周长
我们在椭圆页面学习了椭圆的定义和一些简单属性，在这里我们会学习怎样较为精确地计算它的周长。
周长
奇怪的是，椭圆的周长是很难计算的！
有很多公式，有些公式相当有趣。
注意：a 和 b 是从中心度量的，就像 "半径" 一样。
估计 1
这个估计与正确的答案只有 5% 的差别，但a不能比b长三倍以上（就是说，椭圆不能太 "扁"）：
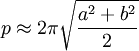
估计 2
著名印度数学家拉马努金找到这个更好的估计：
![椭圆周长估计 pi [ 3(a+b) - sqrt((3a+b)(a+3b))]](images/ellipse-perim-2.gif){kind=small}
估计 3
这个也是拉马努金提出的。我们先求 "h"：
然后代入：
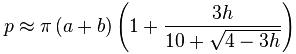
无穷级数 1
这是个绝对精确的公式，但需要计算 "无穷的级数" 来得到绝对精确的答案，所以实际上我们只能得到一个近似值。
然后用这个 "无穷级数" 公式：
![椭圆周长估计 2a pi [ 1 - sigma i=1 到无穷大 ( (2i)!^2/(i!2^i)^4 times e^21/(2i-1))]](images/ellipse-perim-4.gif)
乍看很复杂，但我们可以把它展开为：
![椭圆周长估计 2a pi [ 1 - (1/2)^2 e^2 - (1x3/2x4)^2 e^4 /3 - (1x3x5/2x4x6)^2 e^6 /5 - ... ]](images/ellipse-perim-5.gif)
级数一直延续到无穷大，我们也需要计算很多项的和才能得到一个相当精确的答案。
无穷级数 2
我最喜爱的绝对精确公式（因为用几个项就可以得到非常精确的答案）是：
先求 "h"：
然后代入这个 "无穷级数" 公式：
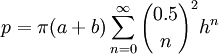
是半整数很可怕的公式！但其实可以展开为：
相加的越多项，答案就越精确（下一项是 25h4/16384，一个相当小的数，在下一个是 49h5/65536，接着是 441h6/1048576）
比较
做一个比较，我用上面的三个估计方法和两个精确方法（只用了头四项，所以也是个估计）来计算这些椭圆的周长：
| 圆 | 线 | |||||
 |
 |
 |
 |
 |
||
| a： | 10 | 10 | 10 | 10 | 10 | |
| b： | 10 | 5 | 3 | 1 | 0 | |
| 估计 1： | 62.832 | 49.673 | 46.385 | 44.65 | 44.429 | |
| 估计 2： | 62.832 | 48.442 | 43.857 | 40.606 | 39.834 | |
| 估计 3： | 62.832 | 48.442 | 43.859 | 40.639 | 39.984 | |
| 级数 1: | 62.832 | 48.876 | 45.174 | 43.204 | 42.951 | |
| 级数 2: | 62.832 | 48.442 | 43.859 | 40.623 | 39.884 | |
| 精确答案*: | 20π | 40 |
* 绝对精确：
- 如果 a=b，椭圆是个圆，周长是 2πa（在这个例子是 62.832……）。
- 如果 b=0（图形是两条直线重叠），周长是 4a（在这个例子是 40）。
所有方法都计算了精确的圆周，但如果椭圆是直线（b=0），只有估计 2 和 3 及 级数 2 的答案接近 40。