多边形的内角
内角是图形内部的角
又一个例子:
三角形
三角形内角的和是 180°
我们用一个三角形来试试:
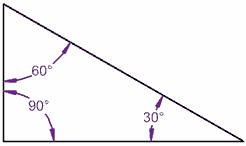
90° + 60° + 30° = 180°
成立!
把一条边倾斜 10°:
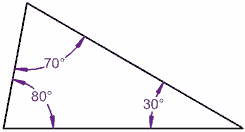
80° + 70° + 30° = 180°
仍然成立!
一个角大了 10°,
另一个角小了 10°
(四边形有四条边)
我们用正方形试试:
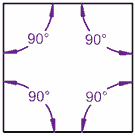
90° + 90° + 90° + 90° = 360°
正方形的内角的和是 360°
把一条边倾斜 10°:
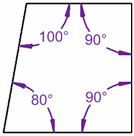
80° + 100° + 90° + 90° = 360°
还是 360°
四边形内角的和是 360°
因为正方形里面有 2个三角形……
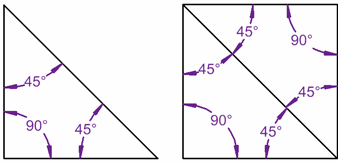
三角形的内角加起来是 180°……
……正方形则是 360° ……
……因为可以用两个三角形来合成一个正方形!
五边形
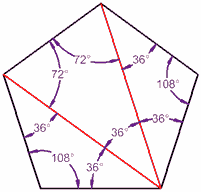
五边形有 5条边,可以由三个三角形组成,所以……
……它的内角的和3是 3 × 180° = 540°
如果是个正五边形(所有角度相等),每个角是 540° / 5 = 108°
(练习:确定每个三角形加起来是 180°,五边形加起来是 540°)
五边形内角的和是 540°
通用规则
每次加一条边(三角形到四边形,四边形到五边形等等),内角的和就增加 180°:
| 如果是个正(规则)多边形(所有边等长,所有角度相等) | ||||
| 图形 | 边 | 内角 的和 |
图形 | 每个角 |
|---|---|---|---|---|
| 三角形 | 3 | 180° | 60° | |
| 四边形 | 4 | 360° | 90° | |
| 五边形 | 5 | 540° | 108° | |
| 六边形 | 6 | 720° | 120° | |
| 七边形 | 7 | 900° | 128.57……° | |
| 八边形 | 8 | 1080° | 135° | |
| 九边形 | 9 | 1260° | 140° | |
| …… | …… | …… | …… | …… |
| 任何多边形 | n | (n-2) × 180° | (n-2) × 180° / n | |
所以通用规则是:
内角的和 = (n-2) × 180°
每个角(正多边形) = (n-2) × 180° / n
来看一个例子:
例子:十边形呢?
 |
这是个正十边形,所以: 每个内角 = 1440°/10 = 144° |