正多边形的属性
多边形
多边形是边是直线的平面(二维)图形,例如三角形、四边形、五边形、六边形等等。
规则
"规则(正)多边形":
否则便是个 不规则多边形。 |
|
在这里我们只谈正多边形。
属性
我们可以谈什么属性?首先,可以谈谈多边形的角。
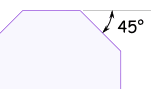 |
外角外角是多边形任何一条边 |
多边形所有的外角加起来是 360°,所以:
每个外角等于 360°/n
(n 是边的个数)
按 play 钮来看看。
(正八边形的)外角
例子:正八边形的外角有多大?
八边形有八条边,所以:
外角 = 360°/n = 360°/8 = 45°
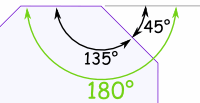 |
内角内角与外角都是在同一条线上,所以它们的和是 180°。 |
内角 = 180° − 外角
外角 = 360°/n,所以:
内角 = 180° − 360°/n
这可以重排成:
| 内角 | = 180° − 360°/n | |
| = (n × 180° / n) − (2 × 180° / n) | ||
| = (n−2) × 180°/n |
所以:
内角 = (n−2) × 180° / n
例子:正八边形的内角有多大?
正八边形有八条边,所以:
外角 = 360° / 8 = 45°
内角 = 180° − 45° = 135°
(正八边形的)内角
我们也可以用:
内角 = (n−2) × 180° / n
= (8−2) × 180° / 8 = 6 × 180° / 8 = 135°
例子:正六边形的内角和外角有多大?
正六边形有六条边,所以:
外角 = 360° / 6 = 60°
内角 = 180° − 60° = 120°
名称:
"外接圆、内接圆、半径和边心距……"
这是多边形 "外面" 和 "里面" 的圆和半径,像这样:
"外面" 的圆叫外接圆,它连接多边形所有的顶点(角)。
外接圆的半径也是多边形的半径。
"里面" 的圆叫内接圆,它刚好接触多边形每一条边的中点。
内接圆的半径是多边形的边心距。
(不是所有的多边形都有这些属性的,但三角形和正多边形有)。
拆成三角形
我们可以把多边形拆成三角形来更具体地分析多边形的属性:
注意:
- 三角形的 "底" 是多边形的边。
- 三角形的 "高" 是多边形的 "边心距"
三角形的面积是底乘高的一半:
一个三角形的面积 = 底 × 高 / 2 = 边长 × 边心距 / 2
整个多边形的面积是所有三角形面积的和(总共有 "n" 个):
多边形面积 = n × 边长 × 边心距 / 2
周长是 = n × 边长,所以:
多边形面积 = 周长 × 边心距 / 2
小三角形
再把三角形一分为二:
小三角形是直角三角形,我们可以用 正弦、余弦和正切函数来分析边长、半径、边心距和 "n" 的关系:
| sin(π/n) = (边长/2) / 半径 | 边长 = 2 × 半径 × sin(π/n) | |
| cos(π/n) = 边心距 / 半径 | 边心距 = 半径 × cos(π/n) | |
| tan(π/n) = (边长/2) / 边心距 | 边长 = 2 × 边心距 × tan(π/n) |
还有很多类似的关系(大部分都是可以互相"转换的"),但在这里我们就谈这么多。
更多面积公式
如果我们只知道边心距,我们可以这样求面积:
小三角形的面积 = ½ × 边心距 × (边长/2)
从上面的 "tan" 公式,我们知道:
边长 = 2 × 边心距 × tan(π/n)
因此:
| 小三角形面积 | = ½ × 边心距 × (边心距 × tan(π/n)) | |
| = ½ × 边心距2 × tan(π/n) |
每边有两个这样的三角形,总共有 2n 个:
多边形面积 = n × 边心距2 × tan(π/n)
如果我们不知道边心距,我们可以用同一个公式,但以半径或者边长为变量:
多边形面积 = ½ × n × 半径2 × sin(2 × π/n)
多边形面积 = ¼ × n × 边长2 / tan(π/n)
数值列表
这是不同多边形的边长、边心距和面积的值(半径为 "1"):
| 种类 | 名称 (正多边形) |
边个数 (n) |
图形 | 内角 | 半径 | 边长 | 边心距 | 面积 |
|---|---|---|---|---|---|---|---|---|
| 三角形 |
等边 三角形 |
3 | 60° | 1 | 1.732 (√3) |
0.5 | 1.299 (¾√3) |
|
| 四边形 |
正方形 | 4 | 90° | 1 | 1.414 (√2) |
0.707 (1/√2) |
2 | |
| 五边形 | 正 五边形 |
5 | 108° | 1 | 1.176 | 0.809 | 2.378 | |
| 六边形 | 正 六边形 |
6 | 120° | 1 | 1 | 0.866 (½√3) |
2.598 ((3/2)√3) |
|
| 七边形 |
正 七边形 |
7 | 128.571° | 1 | 0.868 | 0.901 | 2.736 | |
| 八边形 | 正 八边形 |
8 | 135° | 1 | 0.765 | 0.924 | 2.828 (2√2) |
|
| …… | …… | |||||||
| 五十边形 | 正 五十边形 |
50 | 172.8° | 1 | 0.126 |
0.998 |
3.133 | |
| (注意:数值精确到三位小数) | ||||||||
图
这是上面列表的图,边个数从 3 到 30。
留意当 "n" 越来越大,边心距趋近 1(等于半径),面积趋近 π = 3.14159……和圆形一样。
边长趋近什么?