比例中项
……与射影定理
比例中项
比例中项是这个方程的 x值:
| a | = | x |
| x | b |
"a 比 x 等于 x 比 b"
怎样解 x?
我们可以交叉相乘(把两边乘以 b 和 x)来得到:
|
|
ab = x2 |
现在可以解 x 了:
x = √(ab)
例子:2 和 18 的比例中项是多少?
问题是: "x 的值是多少?"
| 2 | = | x |
| x | 18 |
"2 比 x 等于 x 比 18"
解 x:
x = √(2×18) = √(36) = 6
把 x 代入方程:
| 2 | = | 6 |
| 6 | 18 |
就是说 6 是 "乘法中项"(2 乘 3 是 6,6 乘 3 是 18)

(它也是这两个数的几何平均数。)
再来看一个例子:
例子:5 和 500 的比例中项是多少?
x = √(5×500)
x = √(2500) = 50
就像这样:

直角三角形
我们也可以在直角三角形里应用比例中项。
首先看一个有趣的现象:
- 把直角三角形横放,斜边向下
- 在斜边与对角画高线
- 高线把三角形分成两个三角形,对不对?
这两个三角形相互相似,且和原来的三角形也相似!
因为它们的内角是相同的。
自己来试试:用纸剪一个直角三角形,再沿高线剪开。看看两个三角形是不是相似的。
我们可以用这个属性来解一些问题。
我们有两个定理:
射影定理――第一部分(也称弦高定理)
直角三角形斜边上的高是两条直角边在斜边上的射影的比例中项:
例子:求高度 h(AD)
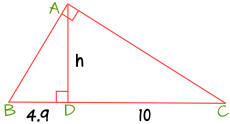
应用:
| 左 | = | 高 |
| 高 | 右 |
在这个例子是:
| 4.9 | = | h |
| h | 10 |
解 h:
射影定理――第二部分
直角边是这条直角边在斜边的射影与斜边的比例中项:
| 和 |
例子:求 x(直角边 AB 的长度)
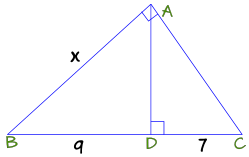
相求斜边:BC = BD + DC = 9 + 7 = 16
用射影定理第二部分:
| 斜边 | = | 直角边 |
| 直角边 | 射影 |
在这个例子是:
| 16 | = | x |
| x | 9 |
解 x:
实例:
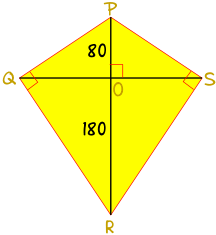
例子:小山喜欢放风筝!
小山想做一只大风筝:
- 风筝的骨架是两根互相垂直的支杆,PR 和 QS,相交点是 O。
- PO = 80厘米,OR = 180厘米。
- 蒙面在 Q 与 S 是个直角。
小山想知道支杆 QS 的长度和蒙面每边的长度。
我们只需要用半个风筝来计算。这是风筝左边,转了 90°
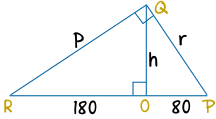
用射影定理第一部分(弦高定理)来求 h::
支杆 QS 的长度 = 2 × 120厘米 = 240厘米
RP = RO + OP = 180厘米 + 80厘米 = 260厘米
用射影定理第二部分来求 r(直角边 QP);
再用射影定理第二部分来求 p(直角边 QR):
告诉小山:支杆 QS 的长度是 240厘米,蒙面的边长是 144厘米 和 216厘米。
万事俱备,只欠东风!