相似

如果两个图形只是大小不同(也许也要移动、旋转或翻转),它们便是相似的。
重点是改变大小
如果一个图形可以通过改变大小(也叫扩大、缩小、压缩、放大,或甚至膨胀)来变成另一个图形,这两个图形便是相似的:
 |
这些图形是相似的! |
|---|
也可能需要旋转、翻转或平移!
有时可能不太容易看到两个图形是不是相似的,因为除了改变大小,你还可能需要旋转、翻转或平移其中一个图形。
| 旋转 | 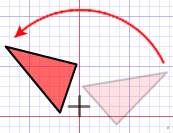 |
转! |
|---|---|---|
| 反射 | 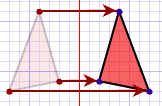 |
翻转! |
| 平移 | 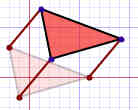 |
移动! |
例子
这些图形对都是相似的:
 |
 |
 |
| 大小改变 | 大小改变和反射 | 大小改变和旋转 |
有什么用?
两个相似图形的:
- 同位角相等,
- 对应的线成比例。
在解几何题时这些很有用,例如:
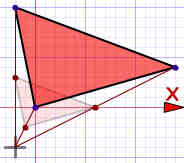
例子:未知的长度是多少?
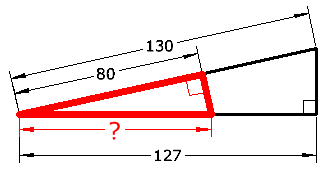
留意红三角形与主三角形的角是相等的……
……都有一个直角和在左下有一个重叠的角
我们可以把红三角形翻转、旋转,然后改变大小,就变成和主三角形一模一样。所以它们是相似三角形。
对应的线的长度成比例。所以:
? = 80 × (130/127) = 81.9
(简单合理的计算!)
全等还是相似?
如果图形的形状和大小都一样,它们便是全等的(但可能旋转、反射或移动了)。所以如果图形变成一模一样:
| 当我们…… | 图形便是…… | |
|---|---|---|
| ……只需要旋转、反射和/或平移 |
全等 |
|
| ……也需要改变大小 |
相似 |
全等图形也是相似的吗?
大部分人(包括我们)都认为 "全等图形也是相似的"。
例子:

我们可以把橙色的图形旋转到和蓝色图形一模一样,所以它们是全等的。
相似不一定需要改变大小!所以这两个图形也是相似的,虽然不用改变大小来使得它们一模一样。