解有理不等式
有理有理式是这样的:
不等式
有时候我们需要解有理不等式,像这些:
| 符号 |
文字 |
例子 |
|---|---|---|
> |
大于 |
(x+1)/(3-x) > 2 |
< |
小于 |
x/(x+7) < -3 |
≥ |
大于或等于 |
(x-1)/(5-x) ≥ 0 |
≤ |
小于或等于 |
(3-2x)/(x-1) ≤ 2 |
解
解不等式和解方程非常相似。。。。。。步骤大部分是相同的。
| 我们尝试找区间, 像图中标签为"<0" 或 ">0"的 |
步骤是这样:
- 找"兴趣点":
- "=0" 的点(根),和
- "垂直渐近线"(函数未定义的地方)
- 在"兴趣点"之间,函数大于零(>0)或 小于零(<0),非此即彼
- 找一点来试试便知道(是 >0 或是 <0)
一个例子:
例子:(3x-10)/(x-4) > 2
第一,把它简化!
但你不能乘以(x-4)
因为"x-4" 可以是正数或负数。。。。。。我们不知道应否改变不等式的方向。 为什么可能要改变不等式的方向?你可以去解不等式看看详细的解释。
我们把"2"移到左边:
(3x-10)/(x-4) - 2 > 0
把 2 乘以 (x-4)/(x-4):
(3x-10)/(x-4) - 2(x-4)/(x-4) > 0
现在有公分母了,我们可以把两个分数拼合在一起:
(3x-10-2x+8)/(x-4) > 0
简化:
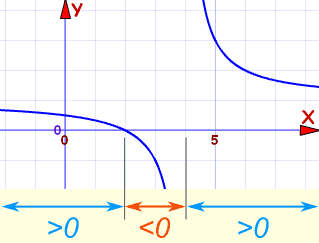
(x-2)/(x-4) > 0
第二,找"兴趣点"。
在 x=2,(0)/(x-4) > 0。这是个"=0"的点,就是它的 根
在 x=4,(x-2)/(0) > 0。这是未定义的
第三,测试一些点来看看函数在兴趣点之间的特征:
在 x=0:
- x-2 = -2,是负数
- x-4 = -4,也是负数
- 所以 (x-2)/(x-4) 一定是正数
以 x=3 和d x=5做同样的计算,我们得到以下的结果:
| x=0 | x=2 | x=3 | x=4 | x=5 | |
|---|---|---|---|---|---|
| x-2 < 0 | x-2 > 0 | x-2 > 0 | |||
| x-4 < 0 | x-4 < 0 | x-4 > 0 | |||
| (x-2)/(x-4) 是 | > 0 | 0 | < 0 | 未定义 | > 0 |
一目了然!
在什么地方 > 0 ?
- 小于 2
- 大于 4
所以结果是:
(-∞, 2) U (4, +∞)
我们不用画图就把问题解决了!
你可以看看(x-2)/(x-4)的图: