有理式

为两个多项式的比的式：

有理式

就好像分数一样，不过是用多项式做成的分数。

其他例子：

(x^3+2x-1)/6x^2 (2x+9)/(x^4-x^2)

还有

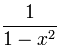1/(1-x^2) 上面的多项式是 "1"，这是允许的。
   
2x^2+3 这也是！这个也可以写成：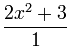
(2x^2+3)/1

但这些不是

不是 不是 上面不是多项式（不能有变量的平方根）
     
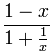不是 不是 多项式里不能有 1/x

一般来说

有理式是两个多项式 P(x) 和 Q(x) 的比：

f(x) = P(x) / Q(x)

可是 Q(x) 不能等于零（在 Q(x)=0 的地方，函数是未定义的）

求有理式的根

"根"（也称为 "零点"）是式等于零的地方：
不等式图y

要求有理式的根，我们只需要求上面的多项式的根，但有理式必须是"最简分式"。

“最简分式”是什么意思？

最简分式

当一个分式的上面（分子）与下面（分母）没有公因式时，分式便是最简分式。

例子：分数

2 6 不是最简分数，
因为 2 和 6 有公因数 "2"

但：

1 3 是 最简分数，
因为 1 和 3 没有公因数

同样，当上面和下面没有公因式时，有理式便是最简分式。

例子：有理式

x3+3x22x 不是最简分式，
因为 x3+3x2 和 2x 有公因式 "x"

但

x2+3x2 是最简分式，
因为 x2+3x 和 2 没有公因式

所以，去求有理式的根：

怎样去求根？去解多项式 看看！

真与假

分数可以是真分数 或 假分数：
分数类型
（"假分数" 没有什么不妥，只不过是其中一个类型）

同样：

有理式亦可以使真分式 或 假分式！

但多项式的“大小”是怎样区分的？

次数！

一元多项式的次数是变量的最大指数。

次数例子：

4x   次数是 1 （没有写指数的变量
的指数是 1）
     
4x3 − x + 3   次数是 3 （x 的最大指数）


我们用以下的准则来定义有理式为真分式 或 假分式：

真分式：上面部分的次数是小于下面部分的次数。

真分式： 1/(x+1)   x/(x^3-1) 次数（上）< 次数（下）

假分式：上面部分的次数是大于或等于下面部分的次数。

假分式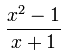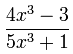： (x^2-1)/(x+1)   (4x^3-3)/(5x^3+1) 次数（上）≥ 次数（下）

我们可以用 多项式长除 来简化假分式

渐近线

有理式可以有 渐近线 （当曲线无限远离原点时所趋近的线）：

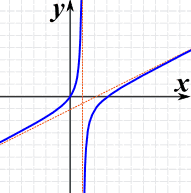
例子：(x2-3x)/(2x-2)

(x2-3x)/(2x-2) 的图有：

  • 在 x=1 的垂直渐近线
  • 在 y=x/2-1 的斜渐近线
   渐近线例子

有理式可以有：

寻找水平或斜渐近线

其实找水平或斜渐近线是相当容易的……

……但这要看上面和下面的多项式的次数的对比。

次数比较大的多项式会增长得比较快。

就像 "真分式" 和 "假分式"，但有四个可能，如下。

 

有理渐近线次数
（在下面，我们会用 x=1000 为例值来分析）

 

我们逐个看看：

上面的次数 小于 下面的次数

下面的多项式会主导有理式的行为，导致一条在零的水平渐近线。

例子：f(x) = (3x+1)/(4x2+1)

当 x 等于 1000：

f(1000) = 3001/4000001 = 0.00075……

x 越大，f(x) 越接近 0

 

上面的次数 等于 下面的次数

上面和下面都不是主导……渐近线是决定于两个多项式的首项。

例子：f(x) = (3x+1)/(4x+1)

当 x 等于 1000：

f(1000) = 3001/4001 = 0.750……

x 越大，f(x) 越趋近 3/4

为什么 3/4？因为 "3" 和 "4" 是每个多项式的 "首项系数"

多项式系数
项以从大到小的指数排列

（严格来说，7 是个常数，但把它视为系数比较容易。）

计算非常容易：

上面的多项式的首项系数除以下面的多项式的首项系数。

这是另一个例子：

例子：f(x) = (8x3 + 2x2 - 5x + 1)/(2x3 + 15x + 2)

次数相同（等于 3）

首项系数：

故此，在 8/2 = 4 有一条水平渐近线

 

上面的次数比下面的次数 大 1

这是一个特别的例子：有斜渐近线，我们需要计算它的方程。

用 多项式长除： 把上面的多项式除以下面的多项式（不理余项）。

例子：f(x) = (3x2+1)/(4x+1)

上面的次数是 2，下面的次数是 1，所以有斜渐近线

用多项式长除，把 3x2+1 除以 4x+1：

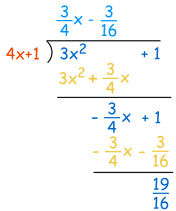
多项式长除

答案是 (3/4)x-(3/16) （不理余项）：

渐近线的 "直线方程" 是：(3/4)x-(3/16)

 

上面的次数比下面的次数大的 多于 1

若上面的多项式的次数比下面的多项式的次数大的多于 1，则不会有水平或斜渐近线。

例子：f(x) = (3x3+1)/(4x+1)

上面的次数是 3，下面的次数是 1。

上面的次数比下面的次数大的多于 1，故此没有水平或斜渐近线。

找垂直渐近线

还有一种渐近线，这种渐近线是由下面的多项式的特性而形成的。

但首先要确定有理式是最简分式！

垂直渐近线  

在任何 下面的多项式子等于零的地方 （任何根）都有一条垂直渐近线。

去看看解多项式来了解怎样求多项式的根

上面的例子：

例子：(x2-3x)/(2x-2)

下面的多项式是 2x-2，可以被因式分解为：

2(x-1)

因式 (x-1) 代表在 x=1 有一条垂直渐近线（因为 1-1=0）

   渐近线例子

完整的例子

例子：画 (x−1)/(x2−9) 的图

我们先来因式分解下面的多项式（它是平方差）：

x−1(x+3)(x−3)

留意：

上面的多项式的根是：+1 （经过 x轴的地方）

下面的多项式的根是：−3 and +3（在这些地方有垂直渐近线）

我们也可以找到经过 y轴的地方，就是 x=0 的地方：

0−1(0+3)(0−3) = −1−9 = 19

上面的次数是小于下面的次数，所以在 0 有水平渐近线

我们可以用上面的资料来画一个草图：

渐近线草图

我们现在可以画图了：

(x-1)/(x^2- 9)

（和 (x-1)/(x2-9) 的图比较一下）

 

 
使用有理式 多项式 代数索引