式的次数

（一元）多项式的次数

多项式是像这样的：

多项式的例子
这个有3项

一元多项式（像 x）的次数是：

……变量最大的指数。

多项式

次数名称

我们可以为次数命名！

次数	名称	例子
0	常数	7
1	线性	x+3
2	二次	x²−x+2
3	三次	x³−x²+5
4	四次	6x⁴−x³+x−2
5	五次	x⁵−3x³+x²+8

例子：y = 2x + 7 的次数是 1，所以它是线性方程

例子：5w² − 3 的次数是 2，所以它是二次

高次数的方程通常比较难解：

解线性方程很容易
解二次方程难一些
解三次方程更难，但可以用公式来帮忙
四次方程也可以解，但公式非常复杂
五次方程没有公式，而且有时不能解！

多元多项式的次数

当一个多项式有多于一个变量，我们需要看每一项。项被 + 或 - 号隔开：

多元多项式例子

每一项：

项的次数是项里每个变量的指数的和，

最大的项的次数就是多项式的次数。

例子：这多项式的次数是什么：

多项式

逐项看：

5xy² 的次数是 3 （x 的指数是 1，y 的指数是 2， 1+2=3）
3x 的次数是 1 （x 的指数是 1）
5y³ 的次数是 3 （y 的指数是 3）
3 的次数是 0 （没有变量）

最大的次数是 3（有两项的次数是 3），所以多项式的次数是 3

例子：这个多项式的次数是什么：

4z³ + 5y²z² + 2yz

逐项看：

4z³ 的次数是 3（z 的指数是 3）
5y²z² 的次数是 4（y 的指数是 2，z 的指数是 2，2+2=4）
2yz 的次数是 2（y 的指数是 1，z 的指数是 1，1+1=2）

最大的指数是 4，所以多项式的次数是 4

写下来

除了说"（某物）的次数是 3"，我们还可以这样写：

当式子是个分数时

我们可以这样算出有理式（分数形式）的次数：上面（分子）的次数减下面（分母）的次数。

以下有三个例子：

计算其他类型的式

警告：高级理念！

有时我们可以用除法来计算一个式子的次数…….

函数的对数除以
变量的对数

……用越来越大的变量来计算，看看答案"趋近"什么值。

（正确来说，我们应该计算 ln(f(x))/ln(x) 在无限远的极限，但在这里我想简单点做）。

附注："ln"是自然对数函数。

一个例子：

例子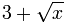：（3 加 x 的平方根）的次数是什么？

我们用越来越大的 x 来计算式的值：

x	ln()	ln(x)	ln() / ln(x)
2	1.48483	0.69315	2.1422
4	1.60944	1.38629	1.1610
10	1.81845	2.30259	0.7897
100	2.56495	4.60517	0.5570
1,000	3.54451	6.90776	0.5131
10,000	4.63473	9.21034	0.5032
100,000	5.76590	11.51293	0.5008
1,000,000	6.91075	13.81551	0.5002

看列表：

当x越来越大， ln(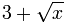) / ln(x) 越来越接近 0.5

故此次数是 0.5 （1/2）

（附注：这和 x^½ = x 的平方根吻合。查看分数指数）)

一些特殊次数

式子	次数
log(x)	0
e^x	∞
1/x	−1
	1/2

		次数是 1（没有指数的变量的指数其实是 1）

		次数是 3 （x 的最大指数）

		次数是 5 （x 的最大指数）

		次数是 2 （z 的最大指数）