无穷级数
无穷个有规律的项的和。
把一个有规律的无穷数列:
| 1 | , | 1 | , | 1 | , | 1 | …… |
| 2 | 4 | 8 | 16 |
(在这例子里每项是上一项的一半)
所有的项加起来:
| 1 | + | 1 | + | 1 | + | 1 | + …… = S |
| 2 | 4 | 8 | 16 |
便成为一个无穷级数。
"级数" 并不是数列,而是数列的和。
(注意:这些点 "……" 代表 "无限延续")
第一个例子
乍看你或会觉得不可能计算出答案,但有时是可以的!
看以上的例子:
| 1 | + | 1 | + | 1 | + | 1 | + ... = 1 |
| 2 | 4 | 8 | 16 |
这是为什么:
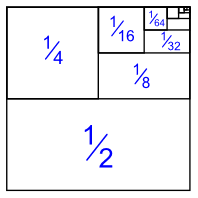
(下面也有一个代数的证明)
记法
我们通常用总合符号来写无穷级数。以上的例子是这样写的:
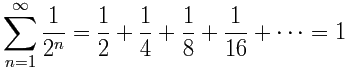
| 这符号(叫总和符号,英语:Sigma)的意思是 "加起来" |
试试把 1/2^n 输入到总和(Sigma)计算器.
另一个例子
| 1 | + | 1 | + | 1 | + | 1 | + ... = | 1 |
| 4 | 16 | 64 | 256 | 3 |
每项是上一项的四分之一,总和是 1/3:
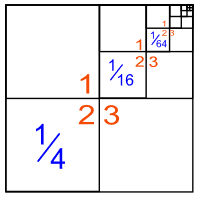
3个空间(1、2和3)里只有 2 被填满,故此和是 1/3。
收敛
有时当我们把每项逐个加上,"和" 便趋向一个有限值。这种无穷级数被称为 "收敛的":
第一个例子:
| 1 | + | 1 | + | 1 | + | 1 | + …… |
| 2 | 4 | 8 | 16 |
加起来像这样:
| 项 | 目前的和 | |
| 1/2 | 0.5 | |
| 1/4 | 0.75 | |
| 1/8 | 0.875 | |
| 1/16 | 0.9375 | |
| 1/32 | 0.96875 | |
| …… | …… |
和趋近 1,所以这个无穷级数是收敛的。
发散
若和列并不收敛,级数便叫做发散。
例子:
1 + 2 + 3 + 4 + ……
加起来是这样:
| 项 | 目前的和 | |
| 1 | 1 | |
| 2 | 3 | |
| 3 | 6 | |
| 4 | 10 | |
| 5 | 15 | |
| …… | …… |
和越来越大,并不趋近一个有限的值。
级数并不收敛,所以它是发散的。
例子:1 − 1 + 1 − 1 + 1 ……
级数不断上下增减,并不趋近一个值,所以它发散。
更多例子
算术级数
若级数里每项与下一项的差是固定的,级数便叫做算术级数。(故此又称:等差级数)
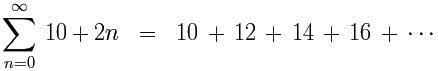
(每项之间的差额是 2。)
几何级数
若级数里每项与下一项的比是固定的,级数便叫做几何级数.(故此又称:等比级数)
上面第一个例子是个几何级数:
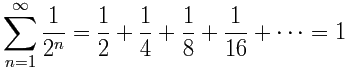
(每项之间的差额是 ½)
我们可以用代数来证明级数等于 1:
| 首先,我们以"S" 代表数列的和: | S = 1/2 + 1/4 + 1/8 + 1/16 + …… | |
| 接着,把S 乘以 ½: | S/2 = 1/4 + 1/8 + 1/16 + 1/32 + …… | |
| 现在把它们相减! | ||
| 1/4 以后的项都互相抵消了。 | ||
| 结果是: | S - S/2 = 1/2 | |
| 简化: | S/2 = 1/2 | |
| 故此: | S = 1 | |
调和级数
这是调和级数:
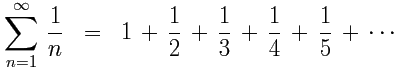
这个级数发散。为什么?把它和另一级数比较:
| 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + …… | ||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||||||
| 等等…… | |||||||||||||||||||
| 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + …… | ||
| 2 | 4 | 4 | 8 | 8 | 8 | 8 | 16 | ||||||||||||
上面的数全都是等于或大于下面的数。
把下面每一组加起来:
| 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | ... | + …… | ||
| 2 | 4 | 4 | 8 | 8 | 8 | 8 | 16 | |||||||||||||
| 1 | + | 1 | + | 1 | + | 1 | + | 1 | + …… = ∞ | |||||||||||
| 2 | 2 | 2 | 2 | |||||||||||||||||
故此,原来的级数也一定是无穷大。
交错级数
一个交错级数的例子(基于上面的调和级数)是:
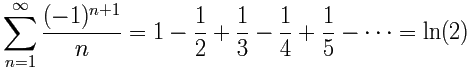
它持续上下增减,但收敛到 2 的 自然对数
高级说明:
要了解为什么,我们先来看看一个面积为 1 的正方形,然后把它和正与负的分数配合,从而显示面积被减小到 y=1/x 的曲线下,在 1 和 2 之间的面积:
用(相信我)积分学,我们可以证明在 y=1/x 曲线下面的这个面积是 ln(2):
(你可以试试去看那些长方形是否真的会组成那个区域!)
更多
还有更多的无穷级数。算出它们是收敛还是发散及收敛到哪个值,往往是个有趣的(也是有挑战性的)练习。