定理、推论、引理
这些是什么?看起来很深奥!
没有什么了不起,它们都是 事实:一些得出来的结果。
- 定理是主要的结果
- 推论是从另一个定理引申出来的定理
- 引理是較小(次要)的结果(没有定理那么重要)
例子
这是几何的例子:
例子:定理、其推论及一个引理!
定理
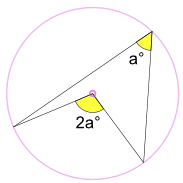
圆周角是 a° 是圆心角 2a° 的一半
这叫 圆周角定理。
证明:连接圆心 O 与 A 点。
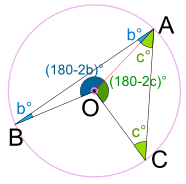
三角形 ABO 是 等边三角形(两等边,两等角),所以:
角 OBA = 角 BAO = b°
因为 三角形的内角的和是 180°,所以:
角 AOB = (180 − 2b)°
三角形 ACO 是等边三角形,所以:
角 OCA = 角 CAO = c°
因为 三角形的内角的和是 180°,所以:
角 AOC = (180 − 2c)°
因为 围绕一点的角度是 360°,所以:
| 角 BOC | = 360° − (180 − 2b)° − (180 − 2c)° |
| = 2b° + 2c° | |
| = 2(b + c)° |
以 a 替代 b + c:
角 BAC = a°,角 BOC = 2a°

证明了定理。
(这是个 "主要" 的结果,所以是个定理。)
推论
(这叫 "同弧的圓周角定理",但其实是"圆周角定理"的推论)
固定端点……在圆周的任何位置,角 a° 都是不变的:
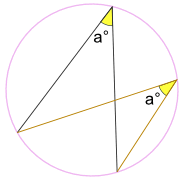
所以,同弧的圓周角是相等的。
引理
(这叫 "半圆上的圆周角定理",但其实它只是"圆周角定理" 的 引理)

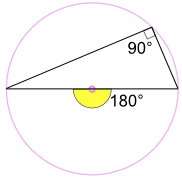
在这个特殊例子里,圆心角是由圆形的直径形成的:
2a° = 180°,所以 a° = 90°
故此,半圆上的圆周角一定是个直角。
(这只不过是个 "小" 的结果,所以是个引理。)
再来一个例子,这个和 勾股定理有关:
例子:
定理
若 m 和 n 为整数,而
- a = m2 − n2
- b = 2mn
- c = m2 + n2
则 a2 + b2 = c2
证明:
| a2 + b2 | = (m2 − n2)2 + (2mn)2 | |
| = m4 − 2m2n2 + n4 + 4m2n2 | ||
| = m4 + 2m2n2 + n4 | ||
| = (m2 + n2)2 | ||
| = c2 |
(这是个 "主要" 的结果。)
推论
a、b 和 c,定义如上,是一组 勾股数
证明:
定理告诉我们:a2 + b2 = c2,
所以 a、b 和 c 是勾股数
(这结果过是从原本的定理 "引申" 出来的。)
引理
若 m = 2 及 n = 1,则得到勾股数 3、4 和 5
证明:
若 m = 2 及 n = 1,则
- a = 22 − 12 = 4 − 1 = 3
- b = 2 × 2 × 1 = 4
- c = 22 + 12 = 4 + 1 = 5
(这是个 "小" 的结果。)