求直角三角形的边长
从已知一边及角度求另一边
我们可以求 直角三角形 的未知边长,若我们已知:
- 一边的长度,和
- 一个角度(除了直角以外)。
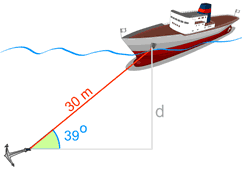
例子:海底深度
船锚定到海底的一点。
已知:
- 锚链的长度(30 m)和
- 锚链与海底之间的角度
我们应该可以计算海的深度!
怎样去做?
我们可以用 正弦、余弦或 正切来做!
但应该用哪个呢?我们可以这样做:
一、看看已知的边是
- 邻边(就是:已知角的其中一边,但不是最长的边),
- 对边(就是:对着已知角的边),
- 斜边(就是:最长的边)。
在这例子:
- 已知边是 斜边
- 求的边是 对边(你可以自己去确定 "d" 是在 39°的角的对面)
二、用以下的公式来决定用正弦、余弦 或 正切:
正弦 |
sin(θ) = 对变 / 斜边 | |
余弦 |
cos(θ) = 邻边 / 斜边 | |
正切A |
tan(θ) = 对边 / 邻边 |
在这个例子,两条边是 对边 和 斜边,所以我们用正弦。
三、把已知值代入正弦方程:
sin 39° = 对边 / 斜边 = = d / 30
四、解方程!
可是,我们怎样去求 sin 39°……?
 |
用计算器。 |
sin 39° = 0.6293…… (我的计算器的结果)
以 0.6293… 代替 sin 39°:
0.6293…… = d / 30
重排,解:
| 开始: | 0.6293…… = d / 30 | |
| 换边: | d / 30 = 0.6293…… | |
| 每边乘以 30: | d = 0.6293…… × 30 | |
| d = 18.88 (保留2个小数位) |
船锚在水深 18.88 m 的海底
逐步来
我们要做四步:
- 一、看看已知的边和需要求的边是对边、邻边还是斜边。
- 二、用上面的公式来决定用 正弦、余弦 或 正切。
- 三、正弦:求 对边/斜边,余弦:求 邻边/斜边, 或 正切:求 对边/邻边。公式里其中一个值是未知的边长。
- 四、用计算器和你的 代数 知识来解
例子
再看一些例子:
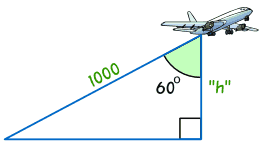
例子:求飞机的高度。
飞机的距离是 1000
角度是 60°
飞机的高度是多少?
小心!60° 的角是在上面,所以 "h" 的边是角的 邻边!
- 一、两条边是 邻边(h)和 斜边(1000)。
- 二、从上面的公式,我们知道应该用余切。
- 三、把值代入余弦方程:
cos 60° = 邻边 / 斜边 = h / 1000
- 四、解:
| 开始: | cos 60°= h/1000 | |
| 换边: | h/1000 = cos 60° | |
| 求 cos 60°: | h/1000 = 0.5 | |
| 每边乘以 1000: | h = 0.5 x 1000 | |
| h = 500 |
飞机的高度 = 500米
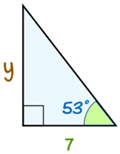
例子:求边 y 的长度:
- 一、两条边是 对边(y)
和 邻边(7)。
- 二从上面的公式,我们知道应该用正切。
- 三、把值代入正切公式:tan 53° = 对边/邻边 = y/7
- 四、解:
| 开始: | tan 53° = y/7 | |
| 换边: | y/7 = tan 53° | |
| 求 tan 53°: | y/7 = 1.32704…… | |
| 每边乘以 7: | y = 1.32704…… × 7 | |
| y = 9.29(保留2位小数) |
边 y = 9.29
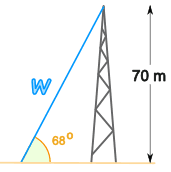
例子:天线杆
天线杆的高度是 70米。
电线以 68°的角度连到杆端。
电线有多长?
- 一、两条边是 对边(70)和 斜边(w)。
- 二、从上面的公式,我们知道应该用 正弦。
- 三、写下正弦的比: sin 68° = 70/w
- 四、解:
未知长度是在分数的下面(分母)!
所以我们需要用不同的计算方法:
| 开始: | sin 68° = 70/w | |
| 每边乘以 w: | w × (sin 68°) = 70 | |
| 每边除以y "sin 68°": | w = 70 / (sin 68°) | |
| 计算: | w = 70 / 0.9271…… | |
| w = 75.5 m (保留一位小数) |
电线的长度 = 75.5 m
版权所有 © 2017 MathsIsFun.com