解 SAS 三角形
"SAS" 的意思是 "(S)ide, (A)ngle, (S)ide"(英语 "Angle" 的意思是 角,"Side" 的意思是 边)
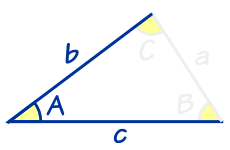 |
"SAS" 的意思是我们知道两个边长和这两边之间的角度。 |
解 SAS 三角形
- 用 余弦定理 来求未知的边长,
- 用 正弦定理 来求较小的未知角度,
- 然后用 三个角的和是 180° 来求剩下的角度。
例 1
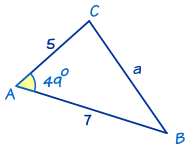
- 角 A = 49°
- 边 b = 5
- 边 c = 7
解这个三角形我们需要找边 a 和角 B 与 C。
先用余弦定理来求边 a:
a2 = b2 + c2 − 2bc cosA
a2 = 52 + 72 − 2 × 5 × 7 × cos(49°)
a2 = 25 + 49 − 70 × cos(49°)
a2 = 74 − 70 × 0.6560……
a2 = 74 − 45.924…… = 28.075……
a = √28.075……
a = 5.298……
a = 5.30 (保留2个小数位)
接着我们用过正弦定理来求其他两个角里较小的一个。
为什么求较小的角?因为就算角度其实是大于 90°,反正弦函数送回的答案都是小于 90°。若我们选较小的角,反正弦函数送回的答案便会是对的(三角形不会有两个大于 90°的角)。注意:较小的角是在较短的边的对面。
选择角 B:
sin B / b = sin A / a
sin B / 5 = sin(49°) / 5.298……
留意到我们没用 a = 5.30 吗?这个数是舍入到只有2个小数位,所以用上一步得到的 5.298……会好得多。计算器里应该还保留了这个数。
sin B = (sin(49°) × 5) / 5.298……
sin B = 0.7122……
B = sin−1(0.7122……)
B = 45.4° (准确到一个小数位)
求角 C 很容易:用 "三角形内角的和是 180°":
C = 180° − 49° − 45.4°
C = 85.6° (准确到一个小数位)
三角形解了――我们知道所有的角度和边长了。
例 2
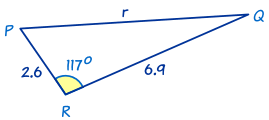
这也是个 SAS 三角形。
首先,用余弦定理来求 r:
r2 = p2 + q2 − 2pq cos R
r2 = 6.92 + 2.62 − 2 × 6.9 × 2.6 × cos(117°)
r2 = 47.61 + 6.76 − 35.88 × cos(117°)
r2 = 54.37 − 35.88 × (−0.4539……)
r2 = 54.37 + 16.289……
= 70.659……
r = √70.659……
r = 8.405……
= 8.41 (准确到2个小数位)
现在用正弦定理。
选较小的角?在这例子不需要!因为角 R 是大于 90°,所以角 P 和 Q 一定是小于 90°。
sin P / p = sin R / r
sin P / 6.9 = sin(117°) / 8.405……
sin P = ( sin(117°) × 6.9 ) / 8.405……
sin P = 0.7313……
P = sin−1(0.7313……)
P = 47.0° (准确到一个小数位)
接着我们用 "三角形内角的和是 180°" 来求角 Q:
Q = 180° − 117° − 47.0°
Q = 16.0° (准确到一个小数位)
这个算法需要时常练习,所以记着……熟能生巧!