解 SSS 三角形
"SSS" 的意思是 "(S)ide, (S)ide, (S)ide"(英语 "Angle" 的意思是 角,"Side" 的意思是 边)
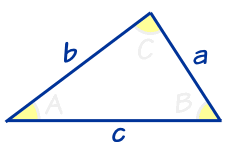 |
"SSS" 的意思是我们知道三个边长,而想求 位知的角度。 |
用 "角e" 的形式的余弦定理:
cos(C) =
a2 + b2 − c2
2ab
cos(A) =
b2 + c2 − a2
2bc
cos(B) =
c2 + a2 − b2
2ca
(以上全是相同的公式,只不过标志不同)
例 1
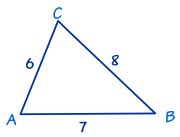
在这个三角形,我们知道三条边:
用余弦定理来求其中一个角。随便哪一个都可以。我们先求 角 A:
cos A = (b2 + c2 − a2) / 2bc
cos A = (62 + 72 − 82) / (2×6×7)
cos A
= (36 + 49 − 64) / 84
cos A
= 0.25
A = cos−1(0.25)
A = 75.5224……°
A = 75.5° 准确到1个小数位。
接下来,我们用另一条边来求另一个角,这里我们再用余弦定理来求 角 B:
cos B = (c2 + a2 − b2)/2ca
cos B = (72 + 82 − 62)/(2×7×8)
cos B = (49 + 64 − 36) / 112
cos B = 0.6875
B = cos−1(0.6875)
B = 46.5674……°
B = 46.6° 准确到1个小数位
最后,我们用"三角形内角的和是 180°"来求 角 C:
C = 180° − 75.5224……° − 46.5674……°
C = 57.9° 准确到1个小数位
三角形解了――我们知道所有的角度和边长了。
三角形可以可以用其他的英语字母而不用 ABC:
例 2
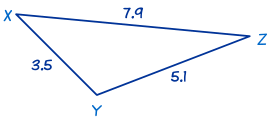
这个也是 SSS 三角形。
在这三角形我们知道三条边:x = 5.1、y = 7.9 和 z = 3.5。先用余弦定理来求 角 X:
cos X = (y2 + z2 − x2)/2yz
cos X = ((7.9)2 + (3.5)2 − (5.1)2)/(2×7.9×3.5)
cos X = (62.41 + 12.25 − 26.01)/55.3
cos X = 48.65/55.3
= 0.8797……
X = cos−1(0.8797……)
X = 28.3881……°
X = 28.4° 准确到1个小数位
再用余弦定理来求 角 Y:
cos Y = (z2 + x2 − y2)/2zx
cos Y = −24.15/35.7
= −0.6764……
cos Y = (12.25 + 26.01 − 62.41)/35.7
cos Y = −24.15/35.7
= −0.6764……
Y = cos−1(−0.6764……)
Y = 132.5684……°
Y = 132.6° 准确到1个小数位。
最后,用 "三角形内角的和是 180°" 来求求 角 Z:
Z = 180° − 28.3881……° − 132.5684……°
Z = 19.0° 准确到1个小数位
另一个方法
最大的角?
为什么要先求最大的角?因为若是这样,其他的两个角便一定是锐角(小于 90°),而正弦定理便会算出正确的答案。
若角是大于 90°,正弦定理 便会相当难用。可能有大于和小于 90°的两个答案(例如:95° 和 85°),但计算器只能算出小的答案。
故此,若我们先用余弦定理来求最大的角,剩下的两个角便一定是小于 90°,用正弦定理来求便会简单一些。
例 3
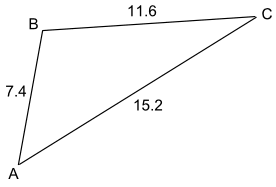
B 是最大的角,所以先用余弦定理来求 B:
cos B = (a2 + c2 − b2) / 2ac
cos B = (11.62 + 7.42 − 15.22) / (2×11.6×7.4)
cos B = (134.56 + 54.76 − 231.04) / 171.68
cos B = −41.72 / 171.68
cos B = −0.2430……
B = 104.1° 准确到1个小数位
用正弦定理,sinC/c = sinB/b 来求角 A:
sin C / 7.4 = sin 104.1° / 15.2
sin C = 7.4 × sin 104.1° / 15.2
sin C = 0.4722……
C = 28.2° 准确到1个小数位
用 "三角形内角的和是 180" 来求角 A:
A = 180° − (104.1° + 28.2°)
A = 180° − 132.3°
A = 47.7° 准确到1个小数位
So A = 47.7°、B = 104.1° 和 C = 28.2°



