科学记数法
科学记数法Standard Form in Britain) -->是一个特别的写数字方法:
| 像这样: | ||
| 或这样: |
我们可以用科学记数法来容易地写下很大或者很小的数。
是怎样的?
例子:700
为什么用科学记数法,700 是写成 7 × 102 的?
700 和 7 × 102 都代表同一个数值,只是写法不同。
例子:4,900,000,000
1,000,000,000 = 109 ,
所以用科学记数法,4,900,000,000 = 4.9 × 109
每个数写成两个部分:
- 所有数位(小数点在第一个数位之后),然后加上
- × 10 的次方,次方把小数点放到适当的位置
(就是要把小数点移多少个位)。
在这个例子里, 5326.6 写成 5.3266 × 103,
因为 5326.6 = 5.3266 × 1000 = 5.3266 × 103
自己来试试
输入一个数来看看它用科学记数法是怎样写的:
现在自己来用科学记数法写数值:
其他写法
3.1 × 10^8
我们可以用 ^ 符号(键盘 6 的上面)。
例子:3 × 10^4 和 3 × 104 是一样的
- 3 × 10^4 = 3 × 10 × 10 × 10 × 10 = 30,000

计算器时常用 "E" 或 "e":
例子:6E+5 和 6 × 105 是一样的
- 6E+5 = 6 × 10 × 10 × 10 × 10 × 10 = 600,000
例子:3.12E4 和 3.12 × 104 是一样的
- 3.12E4 = 3.12 × 10 × 10 × 10 × 10 = 31,200
怎样做
要求科学记数法里的 10 的次方,想:"我要把小数点移动几个位?"
| 如果数大于 10,小数点要向左移,10 的次方便是正数。 | |
|
如果数小于 1,小数点要向右移,10 的次方便是负数。 |
例子:0.0055 写成 5.5 × 10-3
因为 0.0055 = 5.5 × 0.001 = 5.5 × 10-3
例子:3.2 写成 3.2 × 100
我们不需要移小数点,所以次方是 100
但数字是以科学记数法表示的
检验!
把数以科学记数法写下来后,检验来确保正确:
- "数位"部分是在 1 和 10 之间(可以是 1,但不能是 10)
- "次方"部分准确地表示要把小数点移动几个位置
为什么要用科学记数法?
因为在科学和工程学里时常会遇到很大或很小的数,如果用科学记数法来写这些数,处理就会比较容易。
例子:写(和念) 1.3 × 10-9 比 0.0000000013 容易
计算也比较容易:
例子:电脑芯片里空间的面积是 0.00000256米宽、0.00000014米长和 0.000275米高。
空间的体积是多大?
先把三个尺寸都用科学记数法显示:
- 宽: 0.000 002 56米 = 2.56×10-6米
- 长:0.000 000 14米 = 1.4×10-7米
- 高:0.000 275米 = 2.75×10-4米
然后把数字相乘(不理 ×10 部分):
2.56 × 1.4 × 2.75 = 9.856
最后,把 ×10 部分相乘:
10-6 × 10-7 × 10-4 = 10-17(其实很简单,把 −6、−4 和 −7 相加就行了)
答案是 9.856×10-17立方米
在科学里时常使用科学记数法:
例子:太阳、月亮和行星
太阳的质量是 1.988 × 1030 kg.
比写 1,988,000,000,000,000,000,000,000,000,000千克容易
(数字其实没有那多个精确数位。)
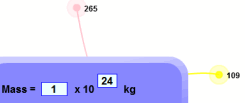
来玩玩!使用科学记数法 |
 |
工程记数法
工程记数法和科学记数法差不多,不过 10 的次数一定是 3 的倍数(例如 103、10-3、1012 等等)。
例子:
- 2,700 写为 2.7 × 103
- 27,000 写为 27 × 103
- 270,000 写为 270 × 103
- 2,700,000 写为 2.7 × 106
例子:0.00012 写为 120 × 10-6
注意 "数字" 部分在 1 与 1,000 之间(可以是 1,但不能是 1,000)。
好处是我们可以用公制数来代替×10 的部分。我们可以用标准词头(例如千或兆),或者用符号(k、M 等)
例子:19,300米是 19.3 × 103米,或 19.3千米
例子:0.00012秒是 120 × 10-6秒,或 120微秒