力的计算

推拉力摔跤运动员

力是推或拉。

通常在物体上的力是平衡的（不平衡的力会导致物体加速）：


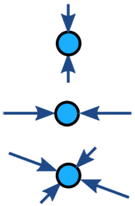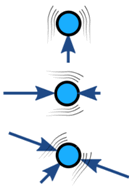平衡		不平衡
无加速		加速度

例子：这个桥塔顶部的力是平衡的（它不在加速）：

悬索桥

悬索向下拉，左右力度相等，与桥塔向上的推力平衡。（桥塔在推吗？当然！如果悬索不是在塔顶，而是在你头顶，你需不需要向上推？）

我们可以做一个数学模型来模拟这些力：

悬索桥力

把代表力的箭头头尾连接起来，箭头刚好环绕一圈，所以所有的力加起来是零（互相抵消）：

悬索桥力
力度平衡。

平衡的力被形容为处于均衡状态：运动也没有改变。

自由体图

首先画个自由体图（也称示力图）)

在悬索桥的例子里，桥顶部的自由体图是：

自由体图

自由体图帮助我们清楚地分析物体承受的力。

例子：高速公路上的汽车

在公路上飞驰的汽车受着什么力？

发动机不停发力，但为什么汽车不无限地加速？

因为驱动汽车前进的力与以下的力成平衡：

空气阻力（即是：空气抗拒被汽车推动），

滚动阻力，也叫滚动摩擦（轮胎抗拒变形）

像这样：

自由体图

W 是汽车的重量，

R₁ 和 R₂ 是轮胎的滚动阻力，

N₁ 和 N₂ 是反作用力（抵消汽车的重量）。

注意：钢轮（像列车的车轮）的滚动阻力比较小，但在公路上就太滑了！

计算

力是矢量。矢量有量值（大小）和放下能：

我们可以用有正确长度与方向的箭头来作为力的模型：

例子：欲穷千里目，更上一层楼

大山站在峡谷观景台上，观景台由一根横梁和一根支柱支撑：

大山的体重是 80千克。

描述所有的力。

我们来看大山站立的地方所承受的力：

大山的体重

地心引力把大山身体的 80千克质量向下拉。

力是质量乘以加速度：F = ma

地球表面的引力加速度是 9.81米/秒²，所以 a = 9.81米/秒²

F = 80千克 × 9.81米/秒²

F = 785牛顿

其他的力

所有的力在平衡状态，所以箭头应该刚好环绕一圈：

我们可以用三角法来求力的数值。
三角形是个直角三角形，我们可以用三角函数来解。

求梁：已知邻边，未知对边，所以我们用正切：

tan(60°) = 梁/785牛顿

梁/785牛顿 = tan(60°)

梁 = tan(60°) × 785牛顿

梁 = 1.732…… × 785牛顿 = 1360牛顿

求支柱：已知邻边，未知斜边，所以我们用余弦：

cos(60°) = 785牛顿 / 支柱

支柱 × cos(60°) = 785牛顿

支柱 = 785牛顿 / cos(60°)

支柱 = 785牛顿 / 0.5 = 1570牛顿

就：

相对于大山的体重，梁和支柱承受的力相当大！

扭力（力矩）

如果只有梁而没有支柱（叫悬臂）呢？

在没有支柱的情况下，有什么力呢？

自由体图像这样：

向上的力 R 抵消了向下的重力。

如果只有这两个力，梁便会转个不停！但是，还有一个 "旋转效应" M，成为力矩（或叫扭力）把它抵消了：

力矩：力乘以垂直距离。

我们知道重力是 785牛顿，我们也需要知道垂直距离，在这个例子里是 3.2米。

M = 785牛顿 × 3.2米 = 2512牛顿米

力矩阻止了梁的旋转。

拿着钓鱼竿时你可以感觉到力矩。

除了举着钓鱼竿的重量，你也要阻止它向下旋转。

摩擦力

斜面上的箱子

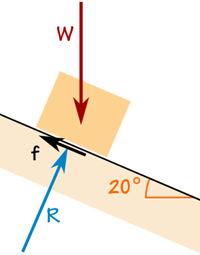
箱子重 100千克。

摩擦力够使箱子静止不动。

反作用力 R 垂直于斜面。

箱子不在加速，所以所有的力互相平衡：

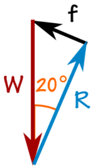
100千克质量向下的地心引力是：

W = 100千克 × 9.81米/秒² = 981牛顿

用三角函数来解。

摩擦 f：

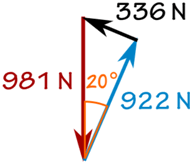
sin(20°) = f/981牛顿

f = sin(20°) × 981牛顿 = 336牛顿

反作用力 N：

cos(20°) = R/981牛顿

R = cos(20°) × 981牛顿 = 922牛顿

结果是：

绘画自由体图提示

尽量简化。通常一个方框就可以了。

代表力的箭头指着力施于物体的方向

用直的箭头来代表力

用弯的箭头来代表力矩

皮皮和森森拉箱子

把大小和方向转换成 x 和 y：

<=>

极坐标里的
矢量 a 笛卡尔坐标里的
矢量 a

你可以去这网页学习转换极坐标和笛卡尔坐标。以下是个简单总结：

将极坐标 (r,θ)
转换为笛卡尔坐标 (x,y) 将笛卡尔坐标 (x,y)
转换为极坐标 (r,θ)

x = r × cos( θ )

y = r × sin( θ )

r = √ ( x² + y²)

θ = tan^-1( y / x )

现在我们来活学活用！

例子：拉箱子

皮皮和森森在拉一个箱子（从上看）：

皮皮向 60°的方向以 200牛顿的力拉

森森向 45°的方向以 120牛顿的力拉

合起来的力是多少，向哪个方向？

把两个矢量头尾连接：

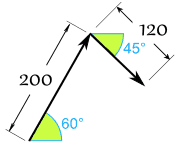
先转换成笛卡尔坐标（保留两个小数）：

皮皮的矢量：

x = r × cos( θ ) = 200 × cos(60°) = 200 × 0.5 = 100

y = r × sin( θ ) = 200 × sin(60°) = 200 × 0.8660 = 173.21

森森的矢量：

x = r × cos( θ ) = 120 × cos(-45°) = 120 × 0.7071 = 84.85

y = r × sin( θ ) = 120 × sin(-45°) = 120 × -0.7071 = −84.85

这就是：

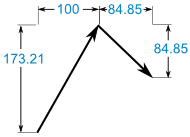
加起来：

(100, 173.21) + (84.85, −84.85) = (184.85, 88.36)

答案是正确的，不过我们把它转换到极坐标，因为问题是用极坐标的：

r = √ ( x² + y²) = √ ( 184.85² + 88.36²) = 204.88

θ = tan^-1( y / x ) = tan^-1( 88.36 / 184.85 ) = 25.5°

结果（舍入后）是：

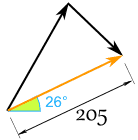
最后结果是这样：

"并肩作战"会好些！

力加速度物理索引

将极坐标 (r,θ) 转换为笛卡尔坐标 (x,y)		将笛卡尔坐标 (x,y) 转换为极坐标 (r,θ)
x = r × cos( θ ) y = r × sin( θ )		r = √ ( x² + y²) θ = tan^-1( y / x )