函数变换
 |
像几何变换,我们也可以把函数移动和伸缩 |
我们先看一个函数,f(x) = x2,但其实我们可以用任何函数:
f(x) = x2
这是一些简单的移动和伸缩转换:
可以把 y值与常数相加来上下移动函数:
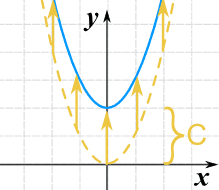
g(x) = x2 + C
注意:用负值的 C 来把线向下移动。
- C > 0 向上移
- C < 0 向下移
把 x值与常数相加就是左右移动:
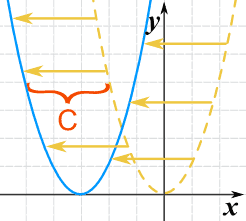
g(x) = (x+C)2
加 C 就是把函数向左(负的方向)移。
为什么?想象你将会在年龄=25 时继承一大笔遗产。如果把这个改成 (age+4) = 25你就会在 21岁时得到遗产。加了 4,发生的时间就早了。
- C > 0 向左移
- C < 0 向右移
但是,一定要把函数里每一个 x 都加上 C (用 x+C 代替 x)。
例子:函数 v(x) = x3 - x2 + 4x
向左移 C 个位,把每一个 x 与 C 相加:
w(x) = (x + C)3 - (x + C)2 + 4(x + C)
记住,加常数:
到 y 就是向上移
到 x 就是向左移
我们可以把函数乘以一个常数来把函数沿 y 的方向伸缩。
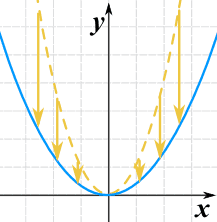
g(x) = 0.35(x2)
- C > 1 伸展
- 0 < C < 1 压缩
我们可以把 x 乘以一个常数来把函数沿 x 的方向伸缩。
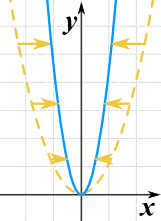
g(x) = (2x)2
- C > 1 压缩
- 0 < C < 1 伸展
注意(与 y 方向不同),常数越大,压缩也越大。
我们可以把函数乘以 −1 来把函数上下翻转:
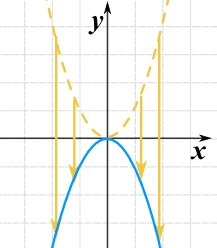
g(x) = −(x2)
这也称为沿 x轴(y=0 的轴)反射
我们可以把负值和伸缩合拼:
例子:乘以 −2 会把函数上下翻转并且沿 y 方向伸展。
我们可以把 x 乘以 −1 来把函数左右翻转:
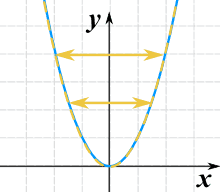
g(x) = (−x)2
真的左右翻转了!但你看不到,因为 x2 是 沿 y轴对称的。这是另一个例子,函数是 √(x):
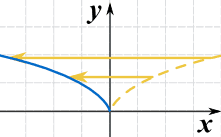
g(x) = √(−x)
这也称为沿 y轴(x=0 的轴)反射
总括
| y = f(x) + C |
|
| y = f(x + C) |
|
| y = Cf(x) |
|
| y = f(Cx) |
|
| y = −f(x) |
|
| y = f(−x) |
|
例子
粒子:函数 g(x) = 1/x
这是一些转换:
| 向上移 2个位: | h(x) = 1/x + 2 | |
| 向下移 3个位: | h(x) = 1/x − 3 | |
| 向右移 4个位: | h(x) = 1/(x−4) 图 | |
| 向左移 5个位: | h(x) = 1/(x+5) | |
| 沿 y 方向伸展 2倍: | h(x) = 2/x | |
| 沿 x 方向压缩 3倍: | h(x) = 1/(3x) | |
| 上下翻转: | h(x) = −1/x |
例子:函数 v(x) = x3 − 4x
这是一些转换:
| 向上移 2个位: | w(x) = x3 − 4x + 2 | |
| 向下移 3个位: | w(x) = x3 − 4x − 3 | |
| 向右移 4个位: | w(x) = (x−4)3 − 4(x−4) | |
| 向左移 5个位: | w(x) = (x+5)3 − 4(x+5) 图 | |
| 沿 y 方向伸展 2倍: | w(x) = 2(x3 − 4x) = 2x3 − 8x | |
| 沿 x 方向压缩 3倍: | w(x) = (3x)3 − 4(3x) = 27x3 − 12x | |
| 上下翻转: | w(x) = −x3 + 4x |
一起做 ……!
我们可以把所有的转换一步做好:
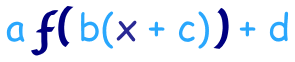
a 垂直伸展/压缩
- |a| > 1 伸展
- |a| < 1 压缩
- a < 0 把图上下翻转
b 是水平伸展/压缩
- |b| > 1 压缩
- |b| < 1 伸展
- b < 0 把图左右翻转
c 是水平移动
- c < 0 向右移
- c > 0 向左移
d 是垂直移动
- d > 0 向上移
- d < 0 向下移