探索立体
这个活动有三部分:
1. 造立体的模型。
2. 探索欧拉公式。
3. 估计表面积和体积。
1. 做模型
你会做以下立体的 模型。 它们全是 多面体 ,前五个叫 柏拉图立体。
你可以用以下的模板 来做立体的模型。 打印在纸上,或者,如果你的打印机可以的话,打印在卡片上会更好。也可以把模板粘在卡片上,再剪下来(待会你会知道我我为什么提议用卡片)。
| 立体 | 模板 | 细节 |
| 四面体 | 四面体 | |
| 立方体 | 立方体 | |
 |
八面体 | 八面体 |
| 十二面体 | 十二面体 | |
| 二十面体 | 二十面体 | |
 |
正四棱锥 | 正四棱锥 |
 |
五棱锥 | 五棱锥 |
你只需 把模板 (连带突出部分)剪下来,顺着线条折叠, 再用胶把突出部分粘到相连的面上。 粘最后一个突出部分时要小心慢慢做, 可能会有些困难。
去 建造指示这页了解多些怎样制作模型。
玩得开心!
2.
探索欧拉公式
完成所有模型后,数数每个立体的 顶点、棱和面 。 你要一边数一边画上标志,这样你便不会忽略或多数。 数的时候,用记号笔把每个顶点涂一个颜色,把每条棱涂另一个颜色,也把每个面涂另一个颜色。 数完以后,把答案填到下面的列表上:
| 立体 | F 面的数量 |
V 顶点的数量 |
E 棱的数量 |
F + V - E |
| 立方体 | ||||
| 四面体 | ||||
| 八面体 | ||||
| 二十面体 | ||||
| 十二面体 | ||||
| 正四棱锥 | ||||
| 五棱锥 |
计算 F + V - E,填进最后一列。
发现什么?
每个答案应该都是一样的。
这个结果叫 欧拉公式。
它适用于所有 多面体。
估计表面积
在上面的列表的”细节“列里链接到的页里有多面体的体积和表面积的公式,而这些公式是相当复杂的。 例如,十二面体的公式是:
十二面体:
表面积
= 3×√(25+10×√5)
× (棱的长度)2
体积
= (15+7×√5)/4
× (棱的长度)3
哇!
很复杂,对不?
我们来看看怎样用我们的模板或模型去估计表面积和体积:
表面积
要估计表面积,我们可以用网格和 数格子。
但用模板会比较容易。 为什么? 你注意到立体的表面积和模板的面积是一样的。 不要算突出部分的面积。 它们不是表面积的一部分。
例子:五棱锥
我用了 1 cm2 的格子.

我估计五棱锥的表面积为大约 98cm2
用同一方法去估计每个立体模型的表面积。
完成以下列表:
| 立体 | 表面积的近似值 (cm2) |
| 立方体 | |
| 四面体 | |
| 八面体 | |
| 二十面体 | |
| 十二面体 | |
| 正四棱锥 | |
| 五棱锥 |
估计体积
在 发现容积活动,你用一个量杯去测量杯子或容器的容积(或体积)。

用水或牛奶来盛满我们这些立体是不妥的。
但我们可以用沙或盐。
如果你没有沙子,拿一包 500g
或 1 lb 的盐。
但盐用完以后就不能用来做菜了!
用一个小漏斗来倒盐。在模型的一个顶点开一个小洞,然后从小洞倒盐进去模型,倒满为止。
你现在应该明白为什么我建议你用卡片来做立体模型了。若你用普通纸张,立体的面就会变形,你的答案便会不准确 。
以二十面体为例:
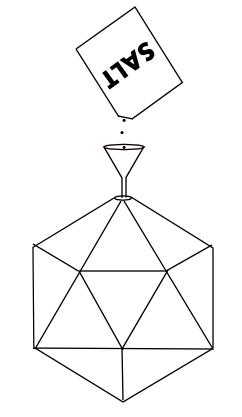
盛满立体模型后,再把盐倒出来到一个量杯里。量杯的单位可能是毫升(ml),1 ml 的容积正好是 1 cm3.
在量杯里的盐的表面要水平和平坦。
看看量杯里的盐的体积,越准确越好。
我做这实验时,盐的体积是 199 cm3,所以二十面体的体积的近似值也是 199 cm3.
每个立体模型都这样做(盐可以重复再用)。
完成以下列表:
| 立体 | 体积近似值 (cm3) |
| 立方体 | |
| 四面体 | |
| 八面体 | |
| 二十面体 | |
| 十二面体 | |
| 正四棱锥 | |
| 五棱锥 |