不等式属性
不等式告诉我们两个值的相对大小。
(你可以先去看不等式入门)
4种不等式
| 符号 |
文字/b> |
例子 |
|---|---|---|
> |
大于 |
x+3 > 2 |
< |
小于 |
7x < 28 |
≥ |
大于或等与 |
5 ≥ x-1 |
≤ |
小于或等与 |
2y+1 ≤ 7 |
符号"指着"较小的数
属性
不等式有不同的属性……每个属性都有特别的名字!
我们在这里把属性列出来,还会举些例子。
注意以下 a、b 和 c 是实数。
传递性
在顺序排列的不等式里,我们可以"跳过"中间的不等式。
若 a < b 并且 b < c,则 a < c
同样:
若a > b 并且 b > c,则 a > c
例子:
- 若 小李 比 小王 年纪大,并且
- 小王 比 璐璐 年纪大
则 小李 也一定比 璐璐 年纪大!
反向属性
我们可以把 a 和 b 调换位置,只要不等号的小(尖)端仍然 "指着" 较小的数,不等式仍是对的。
- 若 a > b 则 b < a
- 若 a < b 则 b > a
例子:小李 比 小王 年纪大,所以 小王 比 小李 年纪小
三分律
"三分律" 说在以下三项里只有一项是对的:
有道理,对不?a 一定是 小于 b 或 等于 b 或 大于 b。一定是其中一个,并且只是一个。
例子:小李 比 小王 有钱
可以写成这样:
a > b
我们也知道:
- 小李 并不 比 小王 少 钱 (非 a<b)
- 小李 并不 与 小王 一样 有钱 (非 a=b)
(那还用说!)
加与减
把 c 加到不等式的两边只不过把一切向同一方向移动,所以不等式不变。
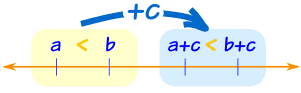
若 a < b, 则 a + c < b + c
例子:小李的硬币比小王的少。
若 李和小王每人多拿 3个硬币,小李的硬币还是比小王的少。
同样:
- 若 a < b,则 a − c < b − c
- 若 a > b,则 a + c > b + c, 并且
- 若 a > b,则 a − c > b − c
所以加(或减)等值到 a 和 b 不会改变不等式
乘与除
把 a 和 b 乘以同一正数,不等式不变。
但若把 a 和 b 乘以同一负数,不等式会倒转过来!
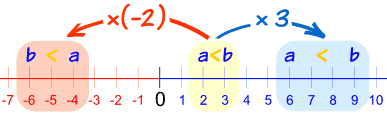
留意到乘以(-2)后,a<b 变成 b<a
但乘以 +3 后,不等式不变
以下是规则:
- 若 a < b,而 c 是正数,则 ac < bc
- 若 a < b,而 c 是负数,则 ac > bc (不等式倒转!)
"正"的例子:
例子:小李的得分,3,低于小王的得分,7。
a < b
如果小李和小王把得分加倍(×2),小李的得分还是低于小王的得分。
2a < 2b
但若乘以负数,情形就变成相反了:
但若得分变成负数,例如 小李 失了 3分,而小王 失了 7分
小李就打得比小王好!
-a > -b
为什么乘以负数会把不等号倒转?
来看看实数直线!
从 3 到 7 是 增加,但从 -3 到 -7 是 减少
 |
|
| -7 < -3 | 7 > 3 |
看到不等号倒转(从 < 变成 >)了吗?
加法逆元
上面我们看到把负号放在 a 和 b 前面就会将不等式倒转方向。这叫"加法逆元":
- 若 a < b 则 -a > -b
- 若 a > b 则 -a < -b
这其实是乘以(-1),所以不等式改变方向。
例子:小李比小王有钱,所以小李的情形比小王好。
但天子下令:"所有的钱变成债,你要做苦工来偿还"
现在小李的情形比小王差。
乘法逆元
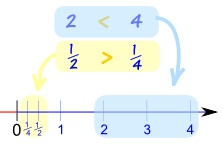 |
取 a 和 b 的 倒数 (1/值)可能改变不等式的方向。 若 a 和 b 都是正数 或 都是负数:
|
例子:小李和小王完成了12千米长的路程。
小李 跑的速度是 6 km/h,而小王步行的速度是 4 km/h。
小李的速度比小王快
6 > 4
但小李的时间是小于小王的时间:
12/6 < 12/4
2 小时 < 3 小时
但当 a 或 b 其中一个是负数 (并非两个都是),不等式的方向不变:
- 若 a < b 则 1/a < 1/b
- 若 a > b 则 1/a > 1/b
平方的非负属性
一个数的平方是大于或等于零的:
a2 ≥ 0
例子:
- (3)2 = 9
- (-3)2 = 9
- (0)2 = 0
永远大于(或等于)零
平方根属性
取平方根并不改变不等式(但 a 和 b 都必须是大于或等于零)。
若 a ≤ b 则 √a ≤ √b
(a,b ≥ 0)
例子:a=4, b=9
- 4 ≤ 9 所以 √4 ≤ √9
