解二次不等式
……和更多……
二次式
标准型的二次方程是这样的:
![]()
标准型的二次方程
(a、b 和 c可以是任何值,除了 a 不能是 0。)
这是一个等式 (=),但有时我们需要解 不等式,像这些:
| 符号 |
文字 |
例子e |
||
|---|---|---|---|---|
> |
大于 |
x2 + 3x > 2 |
||
< |
小于 |
7x2 < 28 |
||
≥ |
大于或等于 |
5 ≥ x2 − x |
||
≤ |
小于或等于 |
2y2 + 1 ≤ 7y |
||
解
解不等式和解方程非常相似……步骤大部分是相同的。
| 解方程时,我们尝试找 点,例如 在图中标签为 "=0"的 |
| 但当我们解不等式时,
我们尝试找区间, 像图中标签为 "<0"的 |
步骤是这样:
- 解 "=0"的点
- 在 "=0"的点之间是区间,在区间里,式子的值是
- 大于零(>0),或
- 小于零(<0))
- 然后找一点来试试(是 >0 或是 <0)
例子:
例子:x2 − x − 6 < 0
x2 − x − 6 有这些简单的因式(我不想弄得太复杂!):
(x+2)(x−3) < 0
首先,找在什么地方等于零:
(x+2)(x−3) = 0
若x = −2 或 x = +3,式子的值是等于零
因为若 x = −2,则 (x+2) 等于是零
,同时
若 x = +3,则 (x−3) 等于零
所以在 −2 和 +3 之间,式子的值一定是
- 大于 零,或
- 一定是小于零
我们暂时不知道是哪一个!
我们在区间里选一个值来试试:
当 x=0: x2 − x − 6
= 0 − 0 − 6
= −6
所以在 −2 和 +3 之间,式子是 小于零。
我们正是找这个区间,所以……
在区间 (−2, 3),x2 − x − 6 < 0
注意:在区间 (−∞,−2) 和 (3, +∞),x2 − x − 6 > 0
这是 x2 − x − 6的图:
|
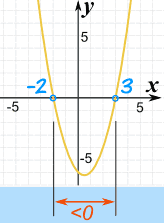 |
|
如果不经过零呢?
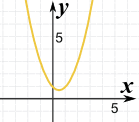 |
这是 x2 − x + 1 的图 没有"=0"的点! 其实这更容易! |
因为线不和 y=0 交叉,它一定是:
所以我们只需测试一个值 (比方 x=0) 来看看是大于零还是小于零。 |
|
"实"例
特技演员将会从20米高的建筑物跳下来。
高速摄像机需要在他离地15米和10米之间拍摄。
摄像机需要在什么时候拍摄?
我们可以用以下的公式来计算距离和时间:
d = 20 − 5t2
- d = 离地距离 (米),
- t = 起跳后时间 (秒)
(注意:若你对这个公式有兴趣,它是从 d = d0 + v0t + ½a0t2 简化而来,其中 d0=20, v0=0, a0=−9.81 是重力加速度。)
我们现在开始。
首先,画一个草图:
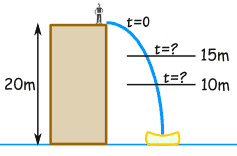 |
我们需要的距离是从 10米 到 15米: 10 < d < 15 d 的公式是: 10 < 20 − 5t2 < 15 |
好了,来解它!
先从每边减 20:
−10 < −5t2 <−5
每边乘以 −(1/5)。我们乘以负数,所以不等式会改变方向……去解不等式看看为什么。
2 > t2 > 1
要写得整齐一点,较小的数应该在左边,较大的在右边。把它们换边(要确保不等号的方向仍然保持正确):
1 < t2 < 2
最后,取平方根(因为所有的值都是正数,所以我们可以这样做):
√1 < t < √2
我们终于可以告诉摄影队:
"从起跳后 1.0 到 1.4秒之间拍摄"
比二次更高的次数
同一概念可以帮我们解更复杂的不等式:
例子:x3 + 4 ≥ 3x2 + x
首先,写成标准型:
x3 − 3x2 − x + 4 ≥ 0
这是 三次方程 (最大指数是立方,x3),很难解,所以我们 画图:
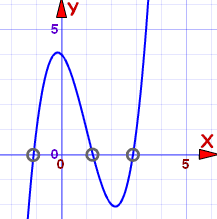
式子等于零的点大约在:
- −1.1
- 1.3
- 2.9
在图上我们也可以看到大于(或等于)零的区间:
- 从 −1.1 到 1.3,和
- 从 2.9 以后
以区间记法来写,这是:
大约: [−1.1, 1.3] U [2.9, +∞)