逆矩阵
请先去这里看矩阵入门。
逆矩阵是什么?
数有倒数:
数的倒数
逆矩阵也是相同的概念,但我们写为A-1
为什么不写成 1/A? 因为我们不除以矩阵!而同时 1/8 也可以写成 8-1
还有其他相似之处:
把数与其倒数相乘的结果是 1
当我们把矩阵与其逆相乘,结果是单位矩阵(就像是矩阵里的"1"):
把逆放在前面的结果是一样的:
单位矩阵
上面我们讲到"单位矩阵"。它是矩阵里的 "1":
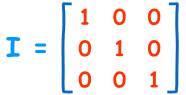
3x3 单位矩阵
- 它是个"方形"矩阵(相同数目的行和列),
- 在对角线是 1,在其他位置是 0。
- 符号是大写字母 I。
单位矩阵可以是 2×2、或 3×3、4×4 等等
定义
这是逆矩阵的定义:
A的 逆(矩阵)是 A-1,仅当:
A × A-1 = A-1 × A = I
但有些矩阵是没有逆矩阵的。
2x2 矩阵
好了,怎样求逆矩阵呢?
2x2 矩阵的逆是:
换句话说:调换 a 和 d 的位置,把 负号放在 b 和 c 前面,然后全部除以矩阵的 行列式 (ad-bc)。
看例子:
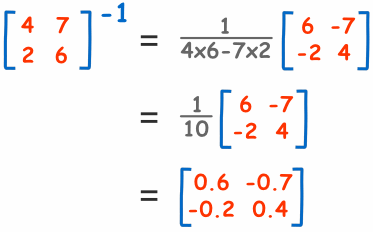
怎样知道答案是对的?
我们上面说过: A × A-1 = I
我们把矩阵与逆矩阵相乘来看看:
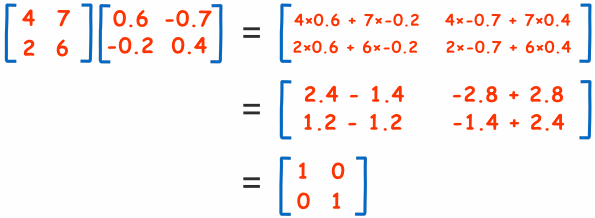
哈!真的得到单位矩阵!所以答案是对的。
A-1 × A = I 也是对的。
你自己来试试把它们相乘,看看可不可以也得到单位矩阵:

我们为什么需要逆矩阵?
以为我们不除矩阵!在矩阵世界里是没有除的概念的。
但我们可以乘以逆矩阵,这和除是相同的。
假设我们不能除以数字。。。。。。
。。。。。。那我我们怎样"把10个苹果分给2个人"呢?
我们可以用 2 的 倒数(等于 0.5):
10 × 0.5 = 5
每人得到 5 个苹果。
矩阵也可以做同样的:
假设我们知道矩阵 A 和 B,而需要求矩阵 X:
XA = B
如果可以每边除以 A (来得到 X=B/A)就最好了,但 我们不能除矩阵。
可是,把每边乘以 A-1 呢?
XAA-1 = BA-1
我们知道 AA-1 = I,所以:
XI = BA-1
拿走 I (和把 "1" 从数子式子 1x = ab 拿走一样):
X = BA-1
得到答案了 (假设可以计算 A-1)
在这个例子中我们要非常小心去做矩阵相乘,因为在矩阵乘法,次序是重要的。AB 几乎永远都不会等于 BA.
实例:公交车与地铁

一帮人坐公交车,车费是小孩¥3,大人¥3.20,总共是¥118.40。
回程他们搭地铁,车费是小孩¥3.50,大人¥3.60,总共是¥135.20。
有几个小孩和几个大人?
我们先把矩阵编排好(小心不要把行和列弄错!):
这和上面的例子一样:
XA = B
去解它我们需要 "A" 的逆:
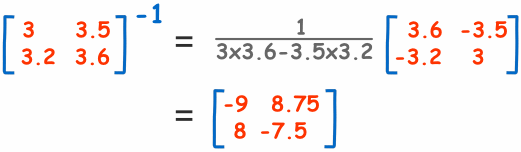
算出逆矩阵后我们便可以这样解:
X = BA-1

有16个小孩和22个大人!
答案很奇妙的出现了。但计算是基于正确的数学逻辑的。
工程师用类似的计算(当然是用大得多的矩阵)来设计楼宇。类似的计算也应用在很多其他的领域,例如在电玩和电脑动画制作里用来显示三维物体。
这也是解线性方程组的一种方法。
计算在电脑中运算,但人必须要了解公式。
次序是重要的
假设我们要求 "X":
AX = B
这和上面的例子不一样! X 现在是在 A 的后面。
在矩阵乘法,次序通常会改变答案。千万不能假设 AB = BA,这几乎一定是错的。
那么我们怎样去解它?用同一方法,但把 A-1 放在前面:
A-1AX = A-1B
我们知道 A-1A= I,所以:
IX = A-1B
拿走 I:
X = A-1B
得到答案了(假设我们可以计算 A-1)
可以这样做,但小心怎样编排矩阵。
正确地编排AX = B是这样:

很酷!我喜欢这个。
留意到与上面的例子比较,行与列调换了("转置"了)
我们需要 "A" 的逆矩阵:
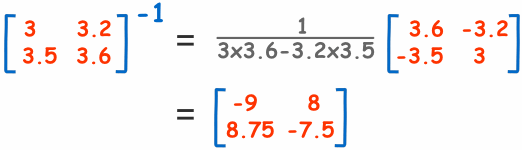
与上面的逆矩阵差不多,但
转置了(行与列调换位置)。
算出逆矩阵后我们便可以这样解:
X = A-1B
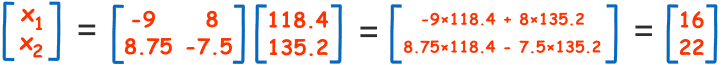
答案没变:16个小孩和22个大人。
矩阵是强大的工具,但一定要编排得正确!
可能没有逆矩阵
首先,矩阵一定要是"方形" (行和列数目相同)才能有逆矩阵。
同时,行列式不能是零 (不然便要除以零了)。看看这个:
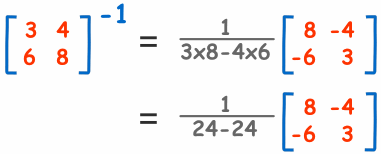
24-24? 等于 0, 1/0 是未定义的。
不能继续做下去了!
这矩阵没有逆矩阵。
这种矩阵叫 "降秩矩阵",就是行列式为零的矩阵。
这合理。。。。。。来看数字:第二行不过是第一行的双倍,没有新的信息。
行列式就是告诉我们这个。
(假想在公交车例子里,地铁的车费全是比公交车贵一半:我们便不能找出大人和小孩的分别。一定要有某些东西来使他们不同,我们才可以算出小孩和大人的数量。)
更大的矩阵
计算 2x2 矩阵的逆是 很容易的。。。。。。与更大的矩阵相比(例如 3x3 和 4x4等)。
计算大矩阵的逆,我们可以用三个方法:
结论
- A 的逆矩阵是 A-1 仅当 A × A-1 = A-1 × A = I
- 求 2x2 矩阵的逆矩阵: 调换 a 和 d 的位置,把 负号 放在 b 和 c 前面,然后全部除以 矩阵的行列式 (ad-bc)。
- 有时候一个矩阵是没有逆矩阵的
