部分分式分解
一个"分解"含有多项式的分数的方法。
什么是部分分式?
我们可以直接这样做:

像这样:
2 x−2 + 3 x+1 = 2(x+1) + 3(x−2) (x−2)(x + 1)
这便可以简化为:
= 2x+2 + 3x−6 x2+x−2x−2
= 5x−4 x2−x−2
(去看使用有理式来了解更多。)
……但倒转过来怎样做?
以下我们将会探索:
怎样求一个分数的"各部分"
("部分分式")。
为什么需要部分分式?
首先……我们为什么需要部分分式?
因为每个部分分式都比较简单。
故此它们可以帮助我们去解比较复杂的分数。比方,在 积分学里,部分分式是非常有用的。
部分分式分解
我现在来做个示范。
这叫"部分分式分解",像这样:
| 一、把下面化为因式。 | ||
| 二、每个因式写成一个部分分式 | ||
| 三、 全部乘以下面的式,之后式子不再是分数了 | ||
四、现在来找常数! 代入下面的式子的根("零点")可能会有用: |
||
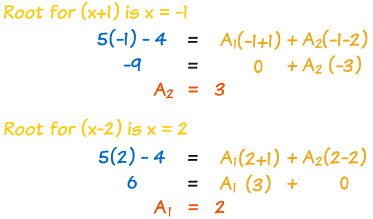 |
||
| 得到答案了: | ||
那相当容易!……老实说,太容易了……
……其实它可以非常困难!
现在我们详细看每一步。
真有理式
这方法只适用于真有理式,就是上面的次数是小于下面的次数的有理式。
次数指数。
- 真:上面的次数是小于下面的次数。
真: 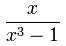
上面的次数是 1
下面的次数是 3 - 假:上面的次数是大于或等于下面的次数。
假: 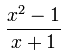
上面的次数是 2
下面的次数是 1
若式子是假的,先去做多项式长除。
把下面化为因式
你自己来把下面化为因式。看代数因式分解。
可是不要化为复数……你可能要把一些因式保留为二次式(叫"不可约二次因式",因为再分解下去就会出现复数了):
例子:(x2-4)(x2+4)
- x2-4 可以分解为 (x-2)(x+2)
- 但 x2+4 只可能分解为复数,所以不要把它分解
我们只能做成这样:
(x-2)(x+2)(x2+4)
故此,因式可以是
- 线性因式,和
- 不可约二次因式
的组合
当你有一个二项式,你便需要包括这部分分式:
B1x + C1(你的二项式)
有指数的因式
有时候你可能得到一个有指数的因式,像 (x-2)3……
每个从 1 以上的指数都需要一个部分分式。
像这样:
例子:
1(x−2)3
有以下的部分分式:
A1x−2 + A2(x−2)2 + A (x−2)3
二次式也可以一样:
例子:
1(x2+2x+3)2
有以下的部分分式:
B1x + C1x2+2x+3 + B2x + C2(x2+2x+3)2
有时候用根也解不了
就算用了下面部分的根(零点),你也可能得到未知的常数。
所以下一步是:
合并同类项(x 的指数是相同的项),然后以它为线性方程组来解。
开玩笑!太复杂了!好,我们来看一个例子:
复杂完整的例子
一个复杂的例子!
x2+15(x+3)2 (x2+3)
- 因为 (x+3)2 的指数是 2,它需要两项(A1 和 A2)。
- 同时,(x2+3) 是个二次式,所以也需要 Bx + C:
x2+15(x+3)2(x2+3) = A1x+3 + A2(x+3)2 + Bx + Cx2+3
全部乘以 (x+3)2(x2+3):
x2+15 = (x+3)(x2+3)A1 + (x2+3)A2 + (x+3)2(Bx + C)
在x = -3 有个根(因为 x+3=0),所以用它试试:
(-3)2+15 = 0 + ((-3)2+3)A2 + 0
简化为:
24 = 12A2
所以 A2=2
把 2 代入 A2 :
x2+15 = (x+3)(x2+3)A1 + 2x2+6 + (x+3)2(Bx + C)
展开:
x2+15 = (x3+3x+3x2+9)A1 + 2x2+6 + (x3+6x2+9x)B + (x2+6x+9)C
合并同类项(x的指数是相同的项):
x2+15 = x3(A1+B)+x2(3A1+6B+C+2)+x(3A1+9B+6C)+(9A1+6+9C)
把每个 x 的指数分开来写,写成线性方程组:
| x3: | 0 | = | A1+B | |
| x2: | 1 | = | 3A1+6B+C+2 | |
| x: | 0 | = | 3A1+9B+6C | |
| 常数: | 15 | = | 9A1+6+9C |
简化并整齐地重排:
| 0 | = | A1 | + | B | ||
| -1 | = | 3A1 | + | 6B | + | C |
| 0 | = | 3A1 | + | 9B | + | 6C |
| 1 | = | A1 | + | C |
好了,去解它!
你可以用你喜欢的方法去解……我就先从第二个方程减去第四个方程:
| 0 | = | A1 | + | B | ||
| -2 | = | 2A1 | + | 6B | ||
| 0 | = | 3A1 | + | 9B | + | 6C |
| 1 | = | A1 | + | C |
把第一个方程乘以 2,把结果从第二个方程减去:
| 0 | = | A1 | + | B | ||
| -2 | = | 4B | ||||
| 0 | = | 3A1 | + | 9B | + | 6C |
| 1 | = | A1 | + | C |
现在我们知道 B = -(1/2)。
所以,从第一个方程我们可以算出 A1 = +(1/2)。
接着,从第四个方程我们可以算出 C = +(1/2)。
最后结果:
| A1=1/2 | A2=2 | B=−(1/2) | C=1/2 |
我们终于得到所有部分分式了:
x2+15 (x+3)2(x2+3) = 1 2(x+3) + 2 (x+3)2 + −x + 1 2(x2+3)
唷!精疲力竭,但终于做好了!
(附注:我花了差不多
一个小时来做这个,因为
当中我犯了两个错误 !)
总结
- 以真有理式来开始(若不是真有理式,先做多项式长除)
- 因式分解下面的式子:
- 线性因式
- 或/和"不可约"二次因式
- 每个因式(和每个因式的次方)写成一个部分分式
- 全部乘以下面的式子
- 用以下方法来解系数:
- 代入下面的式子的根
- 把每个幂(x 的次方)的系数写成一个方程,形成一个线性方程组,然后解它
- 答案就出来了!