多项式：正负号规则

用特别的方法来告诉你多项式有多少个正根和负根。

多项式看起来像这样：

多项式有 "根" （零点）。在这些点，多项式的值为 0：

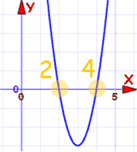
根是在 x=2 和 x=4
这个多项式有 2 个根， 都是正数 （+2 和 +4）)

有时我们不知道根在哪里，但我们可以算出有几个正和负的根……

……只需要数数正负号改变多少次
（从正到负或从负到正）

 

例解：

有几个正根？

首先把多项式的项以从大到小的指数排列 （"零"项可以不理，所以缺了 x⁴ 和 x³ 都没关系）：

-3x⁵ + x² + 4x - 2

接着，数数正负号改变了多少次（从正到负或从负到正）：

在这例子里，正负号改变了2次，所以最多只有2个正数的根（或少于2个）。

所以，这个多项式可以有 2、1或 0 个正根，对不对？

但其实不会有1个正根……下面会解释......

复根

也可能有复数的根。

但是……

复根一定是成双成对的！

成双成对？对，所以可能有：

• 0 个复根，
• 2 个复根，
• 4 个复根，
• 等等

再精确一些

若有复根，正根的个数便会减少 2个（或 4个、或 6个……），换句话说，减少一个偶数个数的根。

在上面的例子，若没有 2个正根，便可能会有 0个正根：

正根的个数是 2 或 0

这是一般的规则：

 

有几个负根？

求有几个负根也是用差不多的算法……

……但首先我们要用 "-x" 来代替"x"，像这样：

然后算出每项你正确的正负号：

• -3(-x)⁵ 就是 +3x⁵
• +(-x)² 就是 +x² （正负号不变）
• +4(-x) 就是 -4x

我们得到这个：

+3x⁵ + x² - 4x - 2

窍门是只有奇指数，像 1、3、5，才会改变正负号。

接下来我们照样数正负号改变的次数：

只有一个改变，所以有 1 个负根。.

但负根的个数可能会更少，因为可能有复根！

慢着……根的个数只能以偶数减少……但 1 不能再以偶数减少了……故此 1 个复返根 是唯一的答案。

根的总数

在 代数基本定理这个网页上，我们说多项式的根的数量是 等于它的次数的 （次数是多项式最高的指数）。

次数是 5， 所以我们知道 总共有 5 个根。

我们目前知道的资料

我们知道以下的资料：

• 正根：2个 或 0个
• 负根：1个
• 总共有：5 个根

最后的结论是：

• 5 个根：2 正、1 负、2 复（一对），或
• 5 个根：0 正、1 负、4 复（两对）

一定要有常数项

最后，一个重点：

若多项式没有常数项，你便要把x分解出来，直到有常数项为止。