代数基本定理
"代数基本定理" 并不是代数的源头,但它描述了多项式的一个有趣特性:
任何 n次多项式……有 n个根
但这可能涉及复数
让我来解释:
多项式的格式像这样:
| 多项式例子 这个多项式有 3 项 |
"根" (或 "零")是 多项式等于零 的点。
故此,三次多项式有三个根(多项式等于零的地方),四次多项式有四个根。依此类推。
例子:求 x2 − 9 的根。
x2 − 9 的次数是 2(x 的最大指数是 2),所以有2个根。
现在我们解它。多项式要等于零:
先把 -9 移到另一边:
每边取平方根:
故此,根是 −3 和 +3
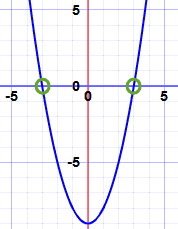
这个也有意思:
多项式可以写成这样:
例子: x2 − 9
根是 r1 = −3 和 r2 = +3 (如上),所以因式是:
(在这个例子中,a等于1,所以我没写下来)
线性因式是 (x+3) 和 (x−3)
所以若我们知道 根是什么,我们也知道 因式是什么。
再来一个例子:
例子: 3x2 − 12
次数是 2,所以有 2 个根。
现在我们解它。多项式要等于零:
3 和 12 有一个公因数 3:
解 x2 - 4:把 -4 移到右边,然后取平方根:
故此,因式是:
3x2 − 12 = 3(x+2)(x−2)
同样,当我们知道多项式的因式,我们亦这道它的根。
例子: 3x2 − 18x + 24
次数是 2,所以有 2 个根。
3x2 − 18x + 24 = a(x−r1)(x−r2)
我知道因式会分解成这样:
3x2 − 18x + 24 = 3(x−2)(x−4)
故此,根(零)是:
- +2
- +4
检验:
3(2)2 − 18(2) + 24 = 12 − 36 + 24 = 0
3(4)2 − 18(4) + 24 = 48 − 72 + 24 = 0
对了!在 x = +2 及 x = +4,多项式是 0
复数
我们可能需要用复数来使多项式等于零。
看一个例子:
例子: x2-x+1
能使它等于零吗?
x2-x+1 = 0
用二次方程解算器,得到的答案是(保留3位小数):
| 0.5 - 0.866i | 和 | 0.5 + 0.866i |
这是复数!但是正确的答案。
故此,因式是:
x2-x+1 = ( x - (0.5-0.866i ) )( x - (0.5+0.866i ) )
复数对
根 r1、r2……等等 可能是实数或复数。
有一个很有趣的现象……
复数根一定是成对的!
如以上例子:
例子: x2-x+1
的根是:
| 0.5 - 0.866i | 和 | 0.5 + 0.866i |
这对根是 共轭复根对(中间的正负号是相反的):
一定成对?对(除非多项式有复数系数,但这里我们只考虑实数系数!)
所以我们会得到:
- 没有 复数根
- 2 个复数根
- 4 个复数根
- ……依此类推
永远不会有 1、3、5、等等
故此,我们知道:
| 次数 | 根 | 可能组合 |
|---|---|---|
| 1 | 1 | 1 实数根 |
| 2 | 2 | 2 实数根、或 2 复数根 |
| 3 | 3 | 3 实数根、 或 1 实数根 和 2 复数根 |
| 4 | 4 | 4 实数根、或 2 实数根 和 2 复数根、或 4 复数根 |
| 等等 | 等等! |
故此:
奇次数(1、3、5、等)的多项式最少有一个实数根……确保没错!
例子: 3x-6
次数是 1。
只有一个实数根
根是 +2:
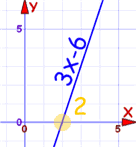 :
:
你可以看到线在某点与 x轴交叉。
但实数也是复数!
我一向说 "实数" 和 "复数",但其实复数包括实数内。
所以若我说有 "2 实数根 和 2 复数根" 时,我其实应该说 "2 纯实数根(没复数部分) 和 2 复数根(有非零的虚数部分)"……
……但那太复杂复了……
……所以请谅解我(可能过分)简单的语言。
不要复数?
若不想要复数,可以把复根对相乘:
(a + bi)(a - bi) = a2 + b2
我们得到没有复数的二次方程……只有实数。
这种不可以再 "约简"(除非用复数)的二次式叫不可约二次式。.
记着,像这样 (x-r1) 的简单因式叫 线性因式
故此,多项式可以被分解成全实数值的因式,它们为:
- 线性因式 和
- 不可约二次式
例子: x3-1
x3-1 = (x-1)(x2+x+1)
分解成:
- 1 线性因式: (x-1)
- 1 不可约二次式: (x2+x+1)
要想继续分解 (x2+x+1),我们需要用复数,所以它是个 "不可约二次式"
我们怎样知道二次式是不可约的?
计算 "判别式":b2 - 4ac
(去看 二次方程 来多些了解判别式。)
若 b2 - 4ac 为负数,二次式有复数根,故此二次式是 "不可约"的
例子: 2x2+3x+5
a = 2、b = 3、c = 5:
b2 - 4ac = 32 - 4×2×5 = 9-40 = -31
判别式是负数,所以这是个 "不可约二次式"
重数
有时因式会出现多于一次,这出现的次数叫根的重数。
例子: x2-6x+9
x2-6x+9 = (x-3)(x-3)
"(x-3)" 出现两次,所以 "3" 这个根的重数是 2
当我们说: "n 次多项式有 n 个根" 时,这些根包括重根在内
例子: x4+x3
应该有 4 个根(和 4 个因式),对不?
因式分解很容易,只需把 x3 分解出来:
x4+x3 = x3(x+1) = x·x·x·(x+1)
有 4 个因式, "x" 重复 3 次。
但乍看只有 2 个根,在 x=-1 和 x=0:
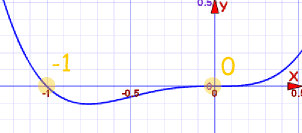
但若我们把重根也算在内,我们便有 4 个根:
- "x" 出现 3 次,所以 "0" 这个根的 重数是 3
- "x+1" 支出项一次,所以 "-1" 这个根的 重数是 1
根的总数 = 3+1 = 4
总结
- n次多项式有 n 个根(多项式等于零的点)
- 多项式可以被因式分解为:a(x-r1)(x-r2)... ,其中 r1 等是多项式的根
- 根可能是复数
- 复数根一定是成对的
- 把复数对相乘会得到 不可约二次式
- 故此,多项式可以被分解成全实数值的因式,它们为:
- 线性因式 或
- 不可约二次式
- 有时因式会出现几次,这个出现的次数是因式的 重数。


