标量与矢量
(……和矩阵)
留心 以下的名词:
距离与位移
- 距离是标量("3 km")
- 位移是矢量 ("3 km 东南")
你可能走了很长的距离,但你的位移可能是很小(甚至是零,若你回到原位)。
速度与速率

- 速度是移动的快慢。
- 速率是向一个方向的速度。
"狗狗旺财跑得有 9 km/h(千米每小时)那么快"是速度的描述。
但是说"旺财 向西跑 9 km/h 那么快"就是速率的描述。
去浏览速度与速率来了解更多。
记法
矢量通常是以粗体字母来记录,像 a 或 b,以区别于标量:
- 所以 c 是矢量,有量值和方向
- 但 c 是标量,像 3 或 12.4
例子: kb 是 标量 k 乘以 矢量 b。
矢量也可以写成它的头(始点)和尾(终点)的字母,上面再放个箭头,像这样:
使用标量
使用标量很容易,当作普通的数来运算就行了.
例子:3 kg + 4 kg = 7 kg
使用矢量
在矢量的网页有详细的解释,这里是简单的概括:
把两个矢量相加――把它们头尾连接起来:

我们也可以用一个矢量减去第二个矢量:
- 先把第二个矢量(要减去的矢量)倒转方向,
- 然后把它们相加:
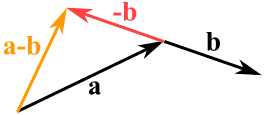
a − b
我们可以把矢量乘以标量(叫"缩放"矢量):
例子:把矢量 m = (7,3) 乘以标量 3
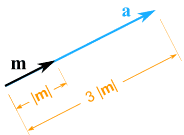 |
a = 3m = (3×7,3×3) = (21,9) |
它还是指向同一方向,但长了 3 倍
极或笛卡儿
矢量可以用两种形式表达:
- 量值和方向 (极)形式,
- 或 x 和 y (笛卡儿)形式
如下:
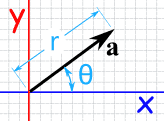 |
<=> | 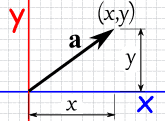 |
| 极坐标里 的矢量 a |
笛卡儿坐标里 的矢量 a |
(在这里了解怎样转换 极坐标和笛卡儿坐标。)
例子:矢量 13 方向 22.6°
极(量值和方向)形式:
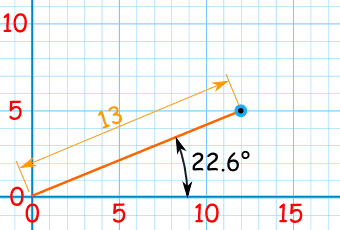
矢量 13 向 22.6°
是大约笛卡儿(x,y)形式的 (12,5):
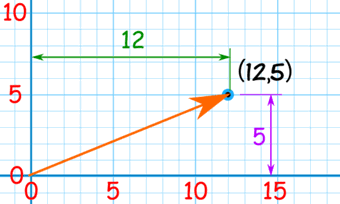
矢量 (12,5)
用 矢量计算器 来体验一下矢量的特性
矢量乘以矢量(点积和叉积)
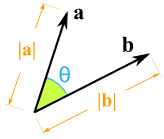 |
怎样把两个矢量相乘?有多种方法! (去看这些网页来了解更多。) |
多于 2维
矢量在 3维或更高维度里也适用:
矢量 (1,4,5)
数列
矢量可以被看作一个数列:
- 2D 空间里用 2个数,例如 (4,7)
- 3D 空间里用 3个数,例如 (1,4,5)
- 依此类推
标量、矢量和矩阵
把标量、矢量与矩阵放在一起,你可以留意到以下有趣的规律:
- 标量是一个数,像 3、-5、0.368等等,
- 矢量是数列(行或列),
- 矩阵是数的排列(一个或以上的行,一个或以上的列)。
矢量也是个矩阵!因为矩阵可以只有一行或一列。
所以矩阵的规则也适用于矢量。
