代数里的平方与平方根
你也许想先看看平方与平方根入门。
平方
要计算一个数的平方,你只需把它与自己相乘……
例子:3 的平方是多少?
| 3 的平方 | = | = 3 × 3 = 9 |
"平方" 通常是写成一个小小的 2:
意思是"4 的平方等于 16"
(小的 2 代表数在乘法里出现了 2 次)
平方根
平方根 是平方的相反:
3 的平方是 9,所以 9 的平方根是 3
就是问:
什么数自乘的积是给定的数?
定义
定义是:
x 的平方根是 平方为 x 的数:
r2 = x
r 是平方根
平方根符号
这是 "平方根" 的符号,它像个对勾(对号), |
使用:
![]()
我们说:"9 的平方根等于 3"
例子:√36 是多少?
答案:6 × 6 = 36,所以 √36 = 6
负数
我们也可以计算负数的平方。
例子:负5的平方是多少?
慢着……"负5的平方" 是什么意思?
- 算5的平方,然后取其负数?
- 还是 (−5) 的平方?
不清晰!答案也是不同的:
- 算5的平方,然后取负数: −(5×5) = −25
- (−5) 的平方: (−5)×(−5) = +25
所以最好用括号: "( )" 来表达。
有意思!
负数的平方是 正数。
正数的平方也一样:
还记的平方根的定义吗?
r2 = x
r 是平方根
我们刚才看到:
(−5)2 = 25
(+5)2 = 25
两个平方根
这就是说……
……25 的平方根 of 可以是 5 ,也可以是 −5
可以有 正 或 负 的平方根!
这很重要,值得牢记!
例子:解 w2 = a
答案:
w = √a 或 w = −√a
主平方根
好,有两个平方根,可是为什么通常都是说: √25 = 5?
因为 √ 是主平方根……就是不是负的那个!
有两个平方根,但√ 这个符号 代表 主平方根。
例子:
36 的平方根是 6 和 −6
但 √36 = 6 (不是−6)
主平方根也叫正平方根。
正负号
| ± | 是一个特殊符号,它的意思是 "正 或 负", |
| 所以: | w = √a 或 w = −√a | |
| 也可以写成: | w = ±√a |
简而言之
| 若: | r2 = x |
|
| 则: | r = ±√x |
这为什么重要?
为什么 "正或负" 重要?因为我们不想忽略任何答案!
例子:解 x2 − 9 = 0
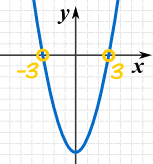
| 开始: | x2 − 9 = 0 | ||
| 把 9 移到右边: | x2 = 9 | ||
| 取平方: | x = ±√9 | ||
| 答案: | x = ±3 |
"±" 符号告诉我们 "−3" 也是个答案。
例子:求 x:(x − 3)2 = 16
| 开始: | (x − 3)2 = 16 | |
| 取平方根: | x − 3 = ±√16 | |
| 计算 √16: | x − 3 = ±4 | |
| 把 3 移到右边: | x = 3 ± 4 | |
| 答案: | x = 7 或 −1 |
检验:(7−3)2 = 42 = 16
检验:(−1−3)2 = (−4)2 = 16
xy 的平方根
当两个数在平方根里相乘,我们可以把它分拆成两个平方根的积:
√xy = √x√y
但 x 和 y 两者都一定要大于或等于 0
例子:√(100×4) 是多少?
| √(100×4) | = √(100) × √(4) |
| = 10 × 2 | |
| = 20 |
同样,√x√y = √xy :
| √8√2 | = √(8×2) |
| = √16 | |
| = 4 |
例子:√(−8 × −2) 是多少?
| √(−8 × −2) | = √(−8) × √(−2) |
| = ??? |
哈!给蒙了!
我们可以用 虚数,但得出来的答案(−4)还是错的
对了……
公式只在 x 和 y 两者都是大于或等于 0 时才管用
所以我们不能用这公式来解这个例子。
这样做就行了:
√(−8 × −2) = √16 = +4
二分之一的指数
平方根也可以写为等于二分之一的 分数指数:
![]()
但 x 一定要大于或等于 0
那么……负数的平方根呢?
结果是 虚数……你可以去那个网页来了解更多。
