分部积分法
分部积分法是一个特别的积分方法,最适用于积分两个函数的积,但在其他的情况下也会有用。
下面会有很多例子,但我们先来看看法则:
∫u v dx = u∫v dx −∫u' (∫v dx) dx
- u 是函数 u(x)
- v 是函数 v(x)
图:
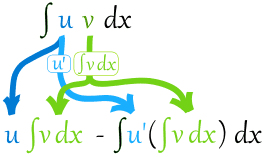
我们现在看一个例子:
例子:∫x cos(x) dx 是什么?
这是 x 乘以 cos(x),所以应该可以用分部积分法。
我们需要先选择哪个函数为 u 和 v:
- u = x
- v = cos(x)
格式和法则里一样了:∫u v dx
求 u 的积分:u' = x' = 1
求 v 的积分:∫v dx = ∫cos(x) dx = sin(x) (见 积分法则)
放进法则里:
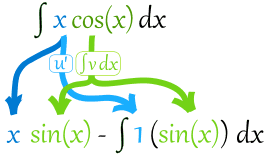
简化,然后解:
步骤是:
- 选 u 和 v
- 求 u 的积分:u'
- 求 v 的积分:∫v dx
- 代入 u, u' and ∫v dx 到:u∫v dx −∫u' (∫v dx) dx
- 简化,然后解
用文字写出来,∫u v dx 是:
(u 积分 v) 减 (u 的倒数,v 的积分)的积分
再看几个例子:
例子: ∫ln(x)/x2 dx 是什么?
先选 u 和 v:
- u = ln(x)
- v = 1/x2
求 u 的积分:ln(x)' = 1/x
求 v 的积分:∫1/x2 dx = ∫x-2 dx = −x-1 = -1/x (基于 幂次方法则)
放进法则里:
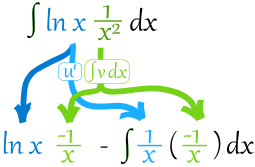
简化:
例子:∫ln(x) dx 是什么?
只有一个函数!我们怎样选 u 和 v ?
没问题!我们选 v 为 "1":
- u = ln(x)
- v = 1
求 u 的积分:ln(x)' = 1/x
求 v 的积分:∫1 dx = x
放进法则里:
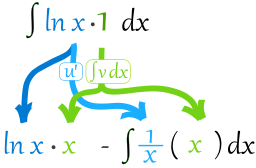
简化:
例子: ∫ex x dx 是什么?
选 u 和 v:
- u = ex
- v = x
求 u 的积分:(ex)' = ex
求 v 的积分: ∫x dx = x2/2
放进法则里:
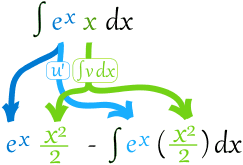
糟了!越来越复杂!
如果我们选不同的 u 和 v 呢?
例子:∫ex x dx (续)
选不同的 u 和 v:
- u = x
- v = ex
求 u 的积分:(x)' = 1
求 v 的积分:∫ex dx = ex
放进法则里:
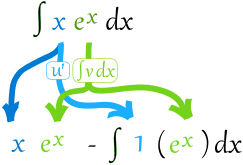
简化:
故事的寓意是:小心选 u 和 v!
选一个微分后比较简单的 u 和积分后不会更复杂的 v。
可以用英语字 I LATE 来帮助记忆。按以下次序来选 u:
- I: (I)nverse 反三角函数,例如 sin-1(x)、cos-1(x)、tan-1(x)
- L: (L)ogarithmic 对数函数,例如 ln(x)、log(x)
- A: (A))lgebraic 代数函数,例如 x2、 x3
- T: (T)rigonometric 三角函数,例如 sin(x)、cos(x)、tan (x)
- E: (E)xponential 指数函数,例如 ex、3x
最后来看一个(复杂的)例子:
例子:∫ex sin(x) dx
选 u 和 v:
- u = sin(x)
- v = ex
求 u 的积分:sin(x)' = cos(x)
求 v 的积分:∫ex dx = ex
放进法则里:
乍看更加复杂,但别着急!我们可以再来一次分部积分法:
选 u 和 v:
- u = cos(x)
- v = ex
求 u 的积分:cos(x)' = -sin(x)
求 v 的积分:∫ex dx = ex
放进法则里:
简化:
现在每边都有同一个积分……
……把右边的搬到左边:
简化:
脚注:"分部积分法" 是从哪里来的?
分部积分法是基于 导数的积法则:
求每边的积分,然后重排:
有些人喜欢上面这个格式,但我喜欢再求 v 的积分,使得左边简单一点: