棱柱
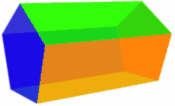
棱柱是有以下属性的多面固体:
- 两个相同的底面
- 平的面
- 沿着其长度(两个底面之间)的截面相同!
截面是横切物体而形成的图形。
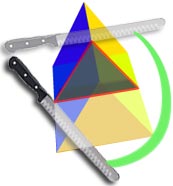
这个物体的截面是个三角形…………
……沿着长度的截面是相同的……
……所以它是个三棱柱。
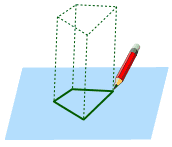
然后想象它从纸向上伸展…… |
 |
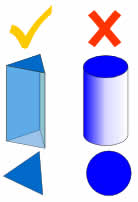
没有曲线!
棱柱是多面体,所有的面都是平面!
没有弯曲的面。
例如,圆柱不是棱柱,因为它有弯曲的侧面.
底面
棱柱的两端互相平行,
叫底面。
侧面
棱柱的侧面是平行四边形
(对边平行的四边形)
这些都是棱柱:
| 正方棱柱: | 截面: |
 |
|
| 立方体: | 截面: |
 |
|
| (对了,立方体是棱柱,因为沿着长度的截面 是个正方形) (也可以去浏览长方体 ) |
|
| 三棱柱 | 截面: |
 |
|
| 五棱柱 | 截面: |
 |
 |
还有很多!
规则与不规则棱柱
上面的例子都是规则(正)棱柱,因为截面都是规则(正)多边形(等角、等边)。
这是个不规则棱柱:
| 不规则五棱柱: | ||
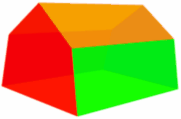 |
 |
|
| 截面 | ||
| 这是 "不规则" 的,因为 截面是 "不规则" 多边形。 |
||
棱柱表面积
| 表面积 = | 2 × 底面积 |
| + 底面周长 × 高 |
例子:棱柱的底面积是 25平方米、底面周长是 24米,高是 12米,表面积是多大?
| 表面积 | = 2 × 底面积 + 底面周长 × 高 | |
| = 2 × 25 平方米 + 24米 × 12米 | ||
| = 50 平方米 + 288平方米 | ||
| = 338平方米 |
(注意:我们有个面积计算器)
棱柱的体积
棱柱的体积是底面积乘高。
体积 = 底面积 × 高
例子:棱柱的底面积是 25平方米,高是 12米,体积是多大?
| 体积 | = 面积 × 高 | |
| = 25平方米 × 12米 | ||
| = 300立方米 |
侧面
棱柱的侧面是平行四边形 (对边平行的四边形)
棱柱可以向一边倾斜,成为一个斜棱柱,但底面仍然是相互平行的,侧面也还是平行四边形!
但如果底面不平行,它便不是棱柱。