函数运算
 |
我们可以把函数相加、相减、相乘和相除! 结果是另一个函数。 |
我们可以来在函数 f(x) 和 g(x) 上做这些运算:
加法 |
我们可以把两个函数相加:
(f+g)(x) = f(x) + g(x)
注意:我们把 f+g 放在 ( ) 里来显示这两个函数都运用在 x 上。
例子:f(x) = 2x+3,g(x) = x2
(f+g)(x) = (2x+3) + (x2) = x2+2x+3
有时候我们需要合并同类项:
例子:v(x) = 5x+1, w(x) = 3x-2
(v+w)(x) = (5x+1) + (3x-2) = 8x-1
另外还要考虑定义域(函数的输入值),我们在下面会解释.
减法 |
我们也可以把两个函数相减:
(f−g)(x) = f(x) − g(x)
例子:f(x) = 2x+3,g(x) = x2
(f−g)(x) = (2x+3) − (x2)
乘法 |
也可以把函数相乘:
(f·g)(x) = f(x) · g(x)
例子:f(x) = 2x+3,g(x) = x2
(f·g)(x) = (2x+3)(x2) = 2x3 + 3x2
除法 |
两个函数相除:
(f/g)(x) = f(x) / g(x)
例子:f(x) = 2x+3,g(x) = x2
(f/g)(x) = (2x+3)/x2
函数复合
| 还有一个特别运算叫函数复合, 去阅读网页来了解更多! |
(g º f)(x) |
定义域
上面讲的都非常简单,但我们还需要考虑函数的定义域。
定义域是函数的所有输入值。
函数要可以运用在所有的输入上,所以你要自己决定用正确的定义域!
例子:√x(x 的平方根)的定义域
负数是没有平方根的(除非用虚数,但在这里我们不用),所以定义域不能包括负数:
√x 的定义域是所有非负实数
在实数直线上像这样:

用集合建构式符号表达就是:
{ x![]()
![]() | x ≥ 0}
| x ≥ 0}
"所有为实数集成员的 x值,满足 x 大于或等于零这个性质的集"
用区间符号表达就是:
[0,+∞)
定义域一定要正确,不然结果就会有问题了!
那么,我们怎样可以得到函数运算后的新定义域呢?
怎样解出新定义域
函数运算的结果需要符合所有运算函数的定义域的限制。

就好像做菜请客:
- 一个客人不吃花生,
- 另一个不吃奶类食品。
所以菜不能有花生,并且不能有奶类食品。
例子:f(x)=√x 和 g(x)=√(3−x)
f(x)=√x 的定义域是 0 及以上:

g(x)=√(3−x) 是小于或等于 3:
![]()
所以新定义域(运算后)是从 0 到 3:
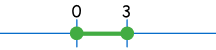
任何其它值都不符合其中一个函数。
换句话说,需要的是两个函数的定义域在哪里相交。
注意:我们可以用集合建构式符号把这个概念写成一行:
Dom(f+g) = { x![]()
![]() | x
| x![]() Dom(f) 和 x
Dom(f) 和 x![]() Dom(g) }
Dom(g) }
意思是:"f 加 g 的定义域是所有在 f 的定义域并且也在 g 的定义域的实数"
不论运算是加、减、乘或除,都需要符合这个规则。除法还有另一个规则。
除法的额外规则
除法还有一个额外规则:
除了跟随以上的规则来限制定义域之外,除法:
(f/g)(x) = f(x) / g(x)
还需要 g(x) 不等于零(不能除以零)。
一个例子:
例子:f(x)=√x,g(x)=√(3−x)
(f/g)(x) = √x / √(3−x)
一、f(x)=√x 的定义域是 0 及以上:

二、g(x)=√(3−x) 的定义域是小于或等于 3:
![]()
三、并且,√(3−x) 不能等于零,所以 x 不能使 3:
![]()
(注意在 3 的位置有个空心圆,意思是不包括 3))
所有的规则一起就是这样:
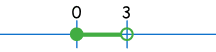
总括
- 函数的加法、减法、乘法和除法和一般运算一样。
- 结果是另一个函数,这个新函数的定义域符合原来两个函数定义域的所有限制.
- 除法还有一个额外规则,就是不能除以零。