圆形方程
圆形很容易画:
画一条与圆心距离是"半径"
的曲线。
故此:
圆形上所有的点与圆心的距离
是相同的。
圆形的定义就是
圆形:在平面上所有与一中点等距的点的集合。
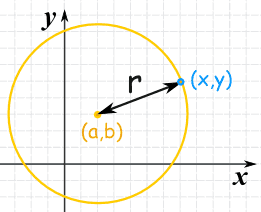
把圆心放在(a,b)。
圆形就是所有与圆心(a,b)的距离为"r"的点(x,y)。
我们可以绝对精确地计算这些点的位置:
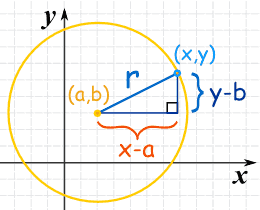
先画一个直角三角形(如图),然后用勾股定理 (a2 + b2 = c2):
(x−a)2 + (y−b)2 = r2
这是圆形方程的"标准式" !
我们很容易便可以看到所有重要的信息:圆心 (a,b) 和 半径 r。
例子:圆心在 (3,4) 和半径为 6 的圆形:
开始:
(x−a)2 + (y−b)2 = r2
代入 (a,b) 和 r:
(x−3)2 + (y−4)2 = 62
接着我们可以用代数运算去简化和重排方程,以得到我们想要的答案。
通用式
你可能不知道你在瞪着圆形的方程!
因为它可能不是像上面的"标准式"那么整齐。
比方,把值代入 a, b 和 r,然后展开
| 开始: | (x-a)2 + (y-b)2 = r2 | |
| 以(例子) a=1, b=2, r=3: |
(x-1)2 + (y-2)2 = 32 | |
| 展开: | x2 - 2x + 1 + y2 - 4y + 4 = 9 | |
| 合并同类项: | x2 + y2 - 2x - 4y + 1 + 4 - 9 = 0 |
结果是:
x2 + y2 - 2x - 4y - 4 = 0
这是"乔装的"圆形方程!
所以若你看到像上面的方程,你应该想:"啊……可能是个圆形!"
用常数来代替数,我们可以把方程写成"通用式":
x2 + y2 + Ax + By + C = 0
把通用式转为标准式
假设我们有通用式的方程(像以上例子):
x2 + y2 - 2x - 4y - 4 = 0
我们怎样把它转变为标准式,像(x-a)2 + (y-b)2 = r2?
答案是:为 x 和 y 配方 (去看看!)……:
| 开始: | x2 + y2 - 2x - 4y - 4 = 0 | |
| 把 x 和 y 集合起来, 放到左边: |
(x2 - 2x) + (y2 - 4y) = 4 | |
配方就是加中间的数的一半的平方。 (也加到右边,以确保方程的平衡!) x 和 y 都做。 |
||
| "x" 配方: | (x2 - 2x + (-1)2) + (y2 - 4y) = 4 + (-1)2 | |
| "y" 配方: | (x2 - 2x + (-1)2) + (y2 - 4y + (-2)2) = 4 + (-1)2 + (-2)2 | |
| 简化: | (x2 - 2x + 1) + (y2 - 4y + 4) = 9 | |
| 最后: | (x - 1)2 + (y - 2)2 = 32 | |
方程转为标准式了!
单位圆
若圆心是在(0,0),并且半径是 1,我们得到:
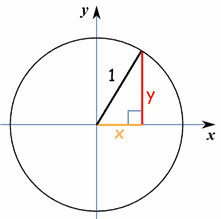 |
(x-a)2 + (y-b)2 = r2 (x-0)2 + (y-0)2 = 12 x2 + y2 = 1 这便是单位圆的方程 |
怎样用手画圆形
一、画圆心 (a,b)
二、画 4 个与圆心的距离是 "半径" 的点,位置为上、下、左、右
三、草拟!
例子:画 (x-4)2 + (y-2)2 = 25
圆形的方程是 (x-a)2 + (y-b)2 = r2
所以圆心是在 (4,2),
而 r2 是 25,所以半径是 √25 = 5
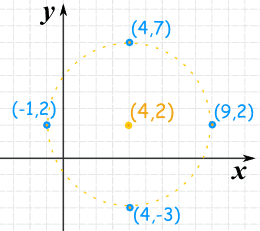
我们来画:
- 圆心: (4,2)
- 上:: (4,2+5) = (4,7)
- 下: (4,2-5) = (4,-3)
- 左: (4-5,2) = (-1,2)
- 右: (4+5,2) = (9,2)
接下来,用手尽量准确地草拟一个漂亮的圆形!
怎样在电脑上画圆形
我们需要把方程写成 "y="的格式。
我们会有两个方程(圆形的上半部和下半部),然后画出来。
例子:画 (x-4)2 + (y-2)2 = 25
圆心在 (4,2),半径是 √25 = 5
重新排列为 "y=":
| 开始: | (x-4)2 + (y-2)2 = 25 | |
| 把 (x-4)2 移到右边: | (y-2)2 = 25 - (x-4)2 | |
| 取平方根: | (y-2) = ± √[25 - (x-4)2] | |
| (注意 "正/负"号…… 可能有两个平方根!) |
||
| 把 "-2" 移到右边: | y = 2 ± √[25 - (x-4)2] |
现在来画这两个方程,就会成为一个圆形:
- y = 2 + √[25 - (x-4)2]
- y = 2 - √[25 - (x-4)2]
看看这圆形的图
你也可以用我们的方程绘图器来一次性绘成圆形。
