多项式的行为
多项式看起来像这样:| 多项式例子 |
连续及平滑
多项式的图有两个主要行为:
多项式的图是连续的。"连续"是个专用词,在微积分中有严谨的定义,但这里我们用这个简单的定义:
 可以笔不离纸画出来
可以笔不离纸画出来
多项式的图也是平滑的,没有尖"角" 或 "波峰"
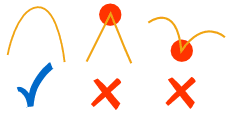
图的特性
我们先画一些图来看看……
……先看一个最简单的图:
f(x) = xn
有一些有趣的事实:
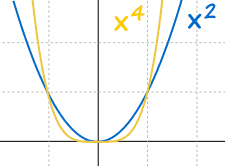 |
若"n"是偶数,便有以下的行为:
|
同时:
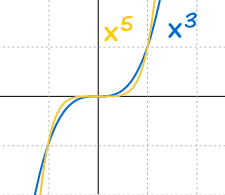 |
若 "n" 是奇数,便有以下的行为:
|
n 次幂函数
加上一个乘数 a,这便成为 "幂函数":
f(x) = axn
f(x) 等于 a 乘以 x 的 n "次方"(n 是指数)
"a" 把图这样改变:
- a 越大,图就越被向 y轴 压缩
- a 越小,图就越被向 y轴的两边扩大
- 负数的a 把图上下倒转
| 例子:f(x) = ax2 a = 2, 1, ½, −1 |
例子:: f(x) = ax3 a = 2, 1, ½, −1 |
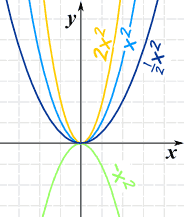 |
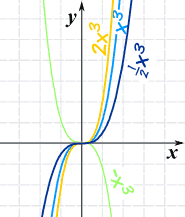 |
我们可以用这些行为来帮助我们绘制多项式的图:
例子:画 y=1−2x7 的图
从最简单的 "奇幂函数" x3 的图 开始,一步一步把它变成 1−2x7
- 我们知道 x3 的样子,
- x7 也差不多,但在零的附近比较平坦,在其他地方则比较陡,
- 把它向 y轴 压缩成 2x7,,
- 上下倒转来得到 −2x7,最后
- 向上移 1 便成为 1−2x7。
像这样:
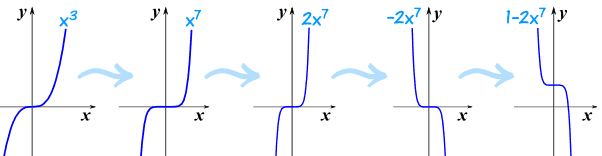
逐步来做就可以得到好结果.
转向点
转向点是当函数是 局部极大值或局部极小值时的 x 值:
一个多项式有几个转向点?
永远不会多过次数减一
例子:4次多项式有 3个(或少于 3个)转向点
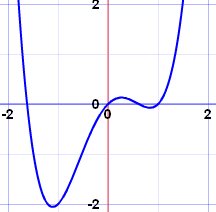 |
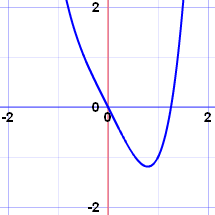 |
|
| x4−2x2+x 有 3 个转向点 |
x4−2x 只有 1 个转向点 |
最多 是 3个,但可能少于 3个。
我们可能不知道它们在哪里,但我们至少知道最多有几个!
当多项式趋近极端时是怎样的
当远离零的时候:
- 在右边(大的 x值),或
- 在左边(大的负 x值)
图便会与 y = axn 的图相似,其中 axn 是 次数最高的项。
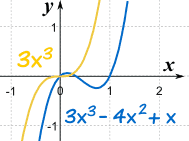
例子:f(x) = 3x3−4x2+x
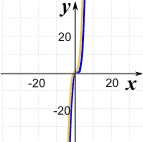
在左边或右边远离原点,图和 3x3的图相似
 |
 |
|
| 在零附近,图是 不同的 |
远离零,图是 相似的 |
这是合理的,因为当 x 的值是很大的时候,x3 比 x2等都大很多
这特性的正式名称是"极端行为模型".
好了,我们讲完了!
总结
- 图是 连续 和 平滑 的
- 偶指数的多项式的行为是:值大于或等于 0; 经过 (0,0)、(1,1) 和 (−1,1);n(指数)越大,在零附近越平坦,在其他地方上升得也比较快。
- 奇指数的多项式的行为是:从x 和 y 同是负数去到 x 和 y 同是正数; 经过 (0,0)、(1,1) 和 (−1,−1);n(指数) 越大,在零附近越平坦,在其他地方上升或下降得也比较快
- 乘以常数:
- 乘以大的常数把图向 y轴压缩
- 乘以小的常数把图向离开 y轴的方向扩大
- 乘以负数把图上下倒转
- 转向点:有不多于 "次数 − 1" 个转向点。
- 极端行为:最大指数的项决定多项式的极端行为