线性及二次方程组

	线性方程是直线的方程。
	二次方程是抛物线的方程至少有一个平方的变量（例如 x²）
	两种方程放在一起便是线性及二次方程组

线性及二次方程组可以用以下的方法来解（寻找方程的线在哪里相交）：

用图（用函数画图器来画图，然后拉大画面）
或用代数

怎样用代数来解

把方程写成 "y =" 的形式
把方程式写成彼此相等
简化成 "= 0" 的形式（像一个标准的二次方程）
解！
用线性方程去求相对的 "y" 值，从而得到答案的 (x,y) 点

举个例：

例子：解以下的方程：

y = x² - 5x + 7
y = 2x + 1

把方程写成 "y=" 的形式：

已经是 "y=" 的形式了，可以跳去下一步

写成彼此相等

x² - 5x + 7 = 2x + 1

简化成 "= 0" 的形式（像一个标准的二次方程）

每边减 2x：x² - 7x + 7 = 1

每边减 1：x² - 7x + 6 = 0

解！

（最难的一步）

你可以去解二次方程看看，在这里我们会用因式分解二次方程：

开始：x² - 7x + 6 = 0

重写 -7x 为 -x-6x：x² - x - 6x + 6 = 0

接着：x(x-1) - 6(x-1) = 0

接着：(x-1)(x-6) = 0

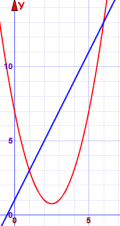
线性及二次

答案是 x=1 和 x=6

用线性方程去求对应的 "y" 值，从而得到答案的 (x,y) 点

对应的 y 值是（也去看看图）：

当 x=1：y = 2x+1 = 3
当 x=6：y = 2x+1 = 13

答案是 (1,3) 和 (6,13)

可以把解法看成三个阶段：

合成二次方程⇒解二次方程⇒求点的值

解

有三个可能：

无实解（线不相交）
有一个实解（直线刚好接触到二次方程的线）
两个实解（像上面的例子）

线性及二次方程不同交叉点

再举个例！

例子：解这两个方程：

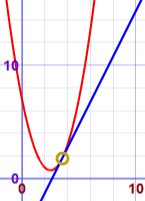
y - x² = 7 - 5x
4y - 8x = -21

把方程写成 "y=" 的形式：

第一个方程是：y - x² = 7 - 5x

每边加上 x²：y = x² + 7 - 5x

第二个方程是：4y - 8x = -21

每边加上 8x：4y = 8x - 21

除以 4：y = 2x - 5.25

写成彼此相等

x² - 5x + 7 = 2x - 5.25

简化成 "= 0" 的形式（像一个标准的二次方程）

每边减 2x：x² - 7x + 7 = -5.25

每边加 5.25：x² - 7x + 12.25 = 0

解！

用二次方程网页里的二次公式：

线性和二次一个交叉点

x = [ -b ± √(b²-4ac) ] / 2a
x = [ 7 ± √((-7)²-4×1×12.25) ] / 2×1
x = [ 7 ± √(49-49) ] / 2
x = [ 7 ± √0 ] / 2
x = 3.5

只有一个答案！（"判别式" 是 0）

用线性方程去求对应的 "y" 值，从而得到答案的 (x,y) 点

对应的 y 值是：

x=3.5: y = 2x-5.25 = 1.75

答案： (3.5,1.75)

实例

轰！

炮弹射出去了，射线是条抛物线：y = 2 + 0.12x - 0.002x²

地面向上倾斜：y = 0.15x

炮弹在哪里着陆？

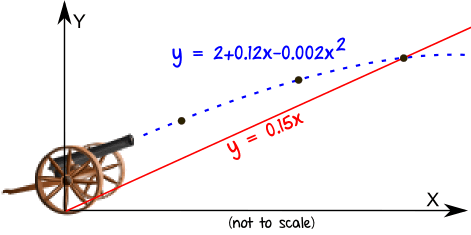
线性二次炮弹

方程已经是 "y =" 的形式，所以只需写成它们彼此相等：

0.15x = 2 + 0.12x - 0.002x²

简化成 "= 0" 的形式：

把全部移到左边：0.002x² + 0.15x - 0.12x - 2 = 0

简化：0.002x² + 0.03x - 2 = 0

乘以 500：x² + 15x - 1000 = 0

解：

分拆 15x 为 -25x+40x：x² -25x + 40x - 1000 = 0

接着：x(x-25) + 40(x-25) = 0

接着：(x+40)(x-25) = 0

x = -40 或 25

不可能有负数的答案，所以 x = 25

用线性方程去求对应的 "y" 值：

y = 0.15 x 25 = 3.75

炮弹在 (25, 3.75) 着陆

你也可以用函数画图器来解：

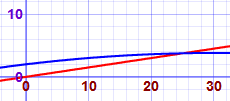线性二次图 .

两个变量都是平方

有时候两个变量都是平方：

例子：求以下两个方程的交叉点：

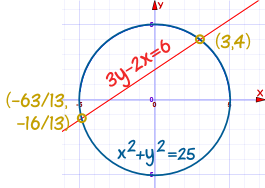
圆形 x² + y² = 25

直线 3y - 2x = 6

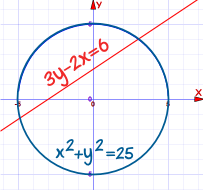
线 3y-2x=6 与圆形 x^2+y^2=25

先把直线写成 "y=" 的形式：

把 2x 移到右边：3y = 2x + 6

除以 3：y = 2x/3 + 2

我们不用把圆形写成 "y=" 的形式，我们可以用 代换法 （以线性式子来代替 "y"）：

把 y = 2x/3 + 2 代入圆形的方程：x² + (2x/3 + 2)² = 25

展开：x² + 4x²/9 + 2(2x/3)(2) + 2² = 25

乘以 9：9x² + 4x² + 2(2x)(2)(3) + (9)(2²) = (9)(25)

简化：13x²+ 24x + 36 = 225

每边减 225：13x²+ 24x - 189 = 0

变成标准的二次形式了。来解它：

13x²+ 24x - 189 = 0

分拆 24x 为 63x-39x：13x²+ 63x - 39x - 189 = 0

接着：x(13x + 63) - 3(13x + 63) = 0

接着：(x - 3)(13x + 63) = 0

所以：x = 3 or -63/13

求 y 值：

把 x = 3 代入线性方程：

3y - 6 = 6
3y = 12
y = 4
其中一点是 (3, 4)

把 x = -63/13 代入线性方程：

3y + 126/13 = 6
y + 42/13 = 2
y = 2 - 42/13 = 26/13 - 42/13 = -16/13
另外一点是 (-63/13, -16/13)

线 3y-2x=6 与圆形 x^2+y^2=25