非直角三角形的面积
有数个不同的方法去求三角形的面积。
已知底和高
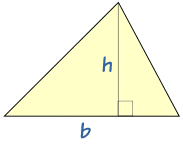
若知道三角形的底和高,求面积便很容易。
就是 底乘高除二
| 面积 = | 1 | bh |
| 2 |
(在 三角形 这页里有详细的解释)
例子:这个三角形的面积是多少?
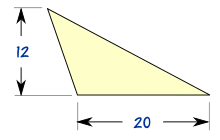
(注意:12 是 高,不是左边的长度)
高 = h = 12
底 = b = 20
面积 = ½ bh = ½ × 20 × 12 = 120
已知三边长度
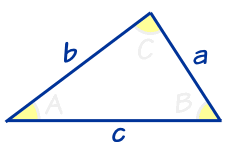 |
有一个公式可以用来求任何已知三边长度的三角形的面积。 你可以去 海伦公式 看看。 |
知道两边长度与夹角
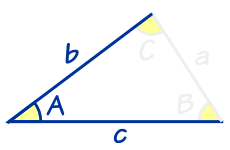 |
若我们知道 两边的长度与夹角,我们可以用另一个公式(其实有三个相等的公式)。 |
视乎哪两条边和夹角,是已知公式可以写成三个不同的形式:
|
||||||
|
||||||
|
它们都是同一个公式,只不过边和夹角不同。
例子:求这个三角形的面积:
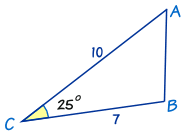
我们先看看已知的资料。
已知: C = 25º,边 a = 7 和 b = 10。
好,开始:
| 开始: | 面积 = | (½)ab sin C | |
| 代入已知值: | 面积 = | ½ × 7 × 10 × sin(25º) | |
| 计算: | 面积 = | 35 × 0.4226... | |
| 面积 = | 14.8 (准确到一个小数位) |
怎样去记
记着英语字母 "abc": 面积 = ½ a b sin C
为什么?
若我们知道底和高,我们便可以得到面积:
面积 = ½ × 底 × 高
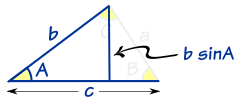 |
在这三角形里:
|
代入公式便是:
面积 = ½ × (c) × (b × sin A)
简化后便是:
| 面积 = | 1 | bc sin A |
| 2 |
改变三角形的标志,我们可以得到:
- 面积 = ½ ab sin C
- 面积a = ½ ca sin B
再举个例:
例子:有多少地
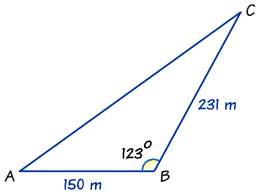
农夫黄先生有一块三角形的地。
栅栏 AB 的长度是 150m。栅栏 BC 的长度是 231m。
栅栏 AB 与 栅栏 BC 之间的角度是 123°。
黄先生的地有多大?
首先,看看有什么已知的资料:
- AB = c = 150m,
- BC = a = 231m,
- 角 B = 123°
所以用这个公式:
| 面积 = | 1 | ca sin B |
| 2 |
| 开始: | 面积 = | ½ ca sinB | |
| 代入已知值: | 面积 = | ½ × 150 × 231 × sin(123º) m2 | |
| 计算: | 面积 = | 17,325 × 0.838... m2 | |
| 面积 = | 14,530 m2 |
黄先生有 14,530m2 大的地