微分方程
例子:这个方程有函数 y 和它的导数
dy
dx
解
解微分方程的意思是求函数 y(或函数 y 的集合)。
有很多 "技巧" 可以用来解微分方程(如有解的话!)。但首先我们要知道:为什么?
微分方程有什么用?
在这个世界上,事物不停变动,而微分方程往往就是形容这些变动的好方法:

例子:兔子!
越多兔子就会越多小兔,小兔长大后又会生小兔。这样,兔子的数量会增长得越来越快!
重要的资料是:
- 在任何时间 t 时兔子的数量 N
- 增长率 r
- 数量变化率
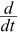 N
N
我们假设一些值:
- 数量 N 是:1000
- 增长率 r 是:每只现有兔子每星期产生 0.01 只新兔子
数量变化率 ![]() N 便是每星期 1000×0.01 = 10 只新兔子。
N 便是每星期 1000×0.01 = 10 只新兔子。
但这只是在一个特定的时间,而没有考虑到兔子数量是在连续不断地增加。
记着:数量越大,新兔子越多!
所以应该说变化率(在任何时间)是增长率乘以在那一刻的数量:
| dN | = rN |
| dt |
这是个 微分方程,因为他有函数 N(t) 和它的导数。
数学是不是很棒?这个短短的方程已可以表达了长长的一句 "数量对于时间的变化率等于增长率乘以数量"。
微分方程可以形容人口变化、热量移动、弹簧震动、放射性物体衰变及很多其他现象。微分方程是形容宇宙里很多事物的正常并合理的方法。
怎样应用微分方程?
微分方程是表达事物的好方法,但用起来并不容易。
所以我们在解微分方程时,尝试把微分方程转变为比较简单的代数式方程(没有微分)。这样我们便可以计算、画图、预测、等等。

例子:复利
钱赚利息。利息可以在固定时间计算,例如每年、每月等等,然后加在余额上。
这叫复利。
但若复利是连续计算的,在每一刻利息都会按比例加在当时的余额上。
余额越大,利息越多。
以 t 为时间、 r 为利率、V 为当前的余额:
| dV | = rV |
| dt |
有趣的是,这和上面兔子的数量是同一个方程!只不过字母不同。数学告诉我们这两个现象的特性是一样的。
解
微分方程是形容事物的好方法,但用起来就不太容易。
但这个微分方程是可以解的,(例如用分离变量法),结果是:
V = Pert
在这里, P 是本金(原来的投资或贷款)。
所以一个连续复利,年期 2 年,年利率 10% 的 ¥1,000 贷款在两年后的余额是:
V = 1000 × e(2×0.1)
V = 1000 × 1.22140...
= $1,221.40 (精确至最接近的一分)
所以虽然微分方程是表达事物的好方法,我们仍需要解了方程才有用。
更多微分方程的例子
费尔哈斯公式

例子:又是兔子!
上面的增长微分方程是:
| dN | = rN |
| dt |
增长不能无穷延续下去,食物始终都会被吃光。
我们加入以下来改良方程:
- 食物可以维持最大的兔子数量 k
数学家费尔哈斯发表了这个方程:
| dN | = rN(1-N/k) |
| dt |
费尔哈斯公式
简谐运动
在物理学中,简谐运动是一种周期运动。在简谐运动中,物体所受的回复力跟位移成正比。简谐运动的一个例子是悬挂在弹簧上的重物。
例子:弹簧和重物
有一个重物悬挂在弹簧上:
- 引力把重物向下拉,
- 弹簧被拉长,张力也跟着增大,
- 然后弹簧弹起,
- 再掉下、弹起、掉下……不断地重复.
有数学来形容这现象!
重物被引力向下拉,而牛顿第二定律 表明:力等于质量乘以加速度:
F = ma
F = m d2xdt2
弹簧把重物向上拉是与弹簧本身被拉长的程度有关(k 是弹簧的刚度,x 是弹簧被拉长的程度):F = -kx
这两个力是相同的:
m d2xdt2 = −kx
是个微分方程!
有函数 x(t) 和它的二阶导数 d2x dt2
注意:我们没有考虑 "阻尼" (由摩擦引致的振动减速),因为这样会更复杂。
我们需要 解 这个微分方程来了解弹簧怎样上下振动。
先分类再去解
怎样去解?

长期以来,很多了不起的人发现了一些特别方法 来解 某些种类 的微分方程。
所以我先需要知道微分方程的种类。
就好像旅行一样:乘搭不同的交通工具可以去不同的地方。去邻近的地方,我们可以走路。有马路我们就可以开车。有河或海洋?我们要乘船了。在另一个银河系?不能去了!(至少暂时不能)
所以我们需要把微分方程分类。
常或偏
第一个主要种类是:
- "常微分方程"(ODE)只有 一个自变量(像 y)
- "偏微分方程"(PDE)有两个或以上自变量。
我们在这里学的是常微分方程!
阶数与次数
接下来我们算出微分方程的阶数与次数:
阶数
阶数是 最高的导数 (是一阶导数还是 二阶导数?等等 ):
例子:
| dy | + y2 = 5x |
| dx |
这个微分方程只有一阶导数 dy dx ,所以是 "一阶"
例子:
| d2y | + xy = sin(x) |
| dx2 |
这个微分方程有个二阶导数 d2y dx2 ,所以是 "二阶"
例子:
| d3y | + x | dy | + y= ex |
| dx3 | dx |
这个有三阶导数 d3y dx3 大于 dy dx ,所以是 "三阶"
次数
次数 是最高导数的指数.
例子:
| ( | dy | ) | 2 + y = 5x2 |
| dx |
最高导数是 dy/dx,它的指数是 2所以这是 "二次"
是个 一阶二次常微分方程
例子:
| d3y | + ( | dy | ) | 2 + y = 5x2 |
| dx3 | dx |
最高导数是 d3y/dx3,但没有指数(其实指数是 1,不过没有写出来),所以这是 "一次"。
(我们不算 dy/dx 的指数 2,因为它不是最高导数)。
所以这是 三阶一次常微分方程
小心!不要把阶数和次数混淆了。有些人说阶数,其实他们的意思是次数!
线性
微分方程是线性的,若变量(和其导数)没有指数或与其他函数相乘。
所以,没有 y2、y3、√y、sin(y)、ln(y) 等等, 只有 y (变量)。
比较正式地说,线性微分方程是以这形式表达的:
| dy | + P(x)y = Q(x) |
| dx |
解
好,我们把微分方程分类了,下一步便是解微分方程。
以下不是所有解微分方程的方法,但你可以用来做学习的起点: