相似三角形
如果两个三角形只是大小不同(也可能要把其中一个翻转或旋转),那么它们便是相似的。
这些三角形都是相似的:
(相等的角用同个数的弧线标记)
它们有些是大小不同的,也有些是旋转或翻转了的。
两个相似三角形:
所有的对应角(同位角)相等
并且
所有的对应边成比例
也要留意对应边在对应角的对面。例如在有两条弧线标记的角对面的边是对应的。
对应边
在相似三角形里,对应边必然是成比例的。
例如:
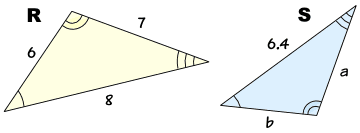
三角形 R 和 S 是相似的。相等的角用相同个数的弧线标记。
哪些是对应的边?
- 长度 7 和 a 是对应的(它们在用一条弧线标记的角的对面)
- 长度 8 和 6.4 是对应的(它们在用两条弧线标记的角的对面)
- 长度 6 和 b 是对应的(它们在用三条弧线标记的角的对面)
求对应边的长度
我们有时可以计算未知的长度。
- 第一步:求对应边的比
- 第二步:用比来求未知边长
例子:求三角形 S 的长度 a 和 b

第一步:求比
我们知道三角形 R 的三条边长和
三角形 S 的一条边长,6.4
6.4 对着用两条弧线标记的角,三角形 R 里的 8 也是对着这个角。
所以 6.4 和 8 是对应的,因此,三角形 S 和三角形 R 的边的比是:
6.4 比 8
我们知道三角形 S 的边长是三角形 R 的对应边长的 6.4/8 倍。
第二步:用比
a 和三角形 R 里的 7 都对着用一条弧线标记的角。
a = (6.4/8) × 7 = 5.6
b 对着用三条弧线标记的角,R 里的 6 也是。
b = (6.4/8) × 6 = 4.8
大功告成!