相似三角形的判定
如果两个三角形的:
- 对应角(同位角)相等,
- 对应边成比例比
但我们不需要知道三条边和三个角……六个里知道两个或三个通常就足够了。
有三个方法去判定两个三角形是不是相似的:AA、SAS 和 SSS:
AA
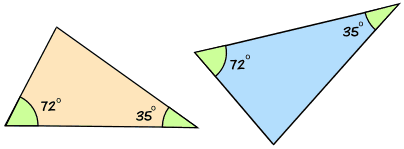
AA 代表 "角、角",英语 "angle, angle",意思是两个三角形有两个角是相同的。
如果一个三角形的两个角与另一个三角形的两个角对应相等,这两个三角形便是相似的。
所以 AA 也可以称为 AAA(因为若两个角相同,则三个角都相同)。
SAS
SAS 代表 "边、角、边",英语 "side, angle, side",意思是在两个三角形里:
- 两组对应边成比例
- 对应的夹角相等。
如果两个三角形的两组对应边成比例,并且对应的夹角相等,这两个三角形便是相似的。
例子:
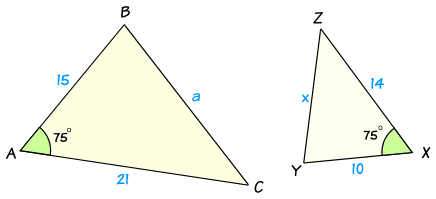
在这个例子里:
- 一对边的比是 21 : 14 = 3 : 2
- 另一对边的比是 15 : 10 = 3 : 2
- 两条边之间的角在两个三角形里都是 75°
这些已经足够使得我们确定这两个三角形是相似的。
用三角学
例子(续)
在三角形ABC 里:
- a2 = b2 + c2 - 2bc cos A
- a2 = 212 + 152 - 2 × 21 × 15 × Cos75°
- a2 = 441 + 225 - 630 × 0.2588……
- a2 = 666 - 163.055……
- a2 = 502.944……
- 所以 a = √502.94 = 22.426……
在三角形XYZ 里:
- x2 = y2 + z2 - 2yz cos X
- x2 = 142 + 102 - 2 × 14 × 10 × Cos75°
- x2 = 196 + 100 - 280 × 0.2588……
- x2 = 296 - 72.469……
- x2 = 223.530……
- 所以 x = √223.530…… = 14.950……
我们看看这两条边的比:
a : x = 22.426^ : 14.950^ = 3 : 2
和上面的一样!
注意:我们也可以用正弦定理来说明另外两条边是等长的。
SSS
SSS 代表 "边、边、边",英语 "side, side, side",意思是两个三角形的三组对应边成比例。
如果两个三角形的三组对应边成比例,那么这两个三角形便是相似的。
例子:
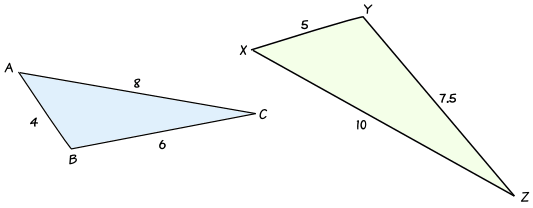
在这个例子里,对应边的比是:
- a : x = 6 : 7.5 = 12 : 15 = 4 : 5
- b : y = 8 : 10 = 4 : 5
- c : z = 4 : 5
比是相同的,所以三角形是相似的。
用三角学
我们可以用三角学里的 余弦定理来显示说明两个三角形的角是相等的:
在三角形ABC 里:
- cos A = (b2 + c2 - a2)/2bc
- cos A = (82 + 42 - 62)/(2× 8 × 4)
- cos A = (64 + 16 - 36)/64
- cos A = 44/64
- cos A = 0.6875
- 所以角A = 46.6°
在三角形XYZ 里:
- cos X = (y2 + z2 - x2)/2yz
- cos X = (102 + 52 - 7.52)/(2× 10 × 5)
- cos X = (100 + 25 - 56.25)/100
- cos X = 68.75/100
- cos X = 0.6875
- 所以角X = 46.6°
A 和 X 是相等的!
同样,我们也可以说明角B 和角Y 相等,并且角C 和角Z 也相等。