相似三角形定理
一、平行线截比例线段定理
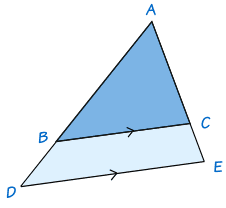
设 ADE 为任何三角形,而线段BC 平行于 DE,则 AB/BD = AC/CE
要证明这个定理,画线段BF 平行于 AE 来形成平行四边形BCEF:
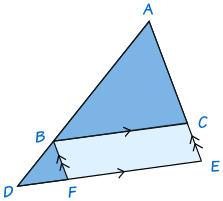
三角形 ABC 和 BDF 有相等的角,所以是相似三角形(为什么?去相似三角形的判定看 AA 的部分。)
- 边AB 对应边BD,边AC 对应边BF。
- 所以 AB/BD = AC/BF
- 而且 BF = CE
- 所以 AB/BD = AC/CE
角平分线定理
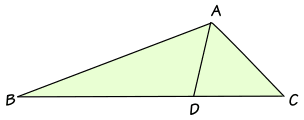
设 ABC 为任何三角形,而AD 平分角BAC,则 AB/BD = AC/DC
要证明这个定理,可以这样标记三角形:
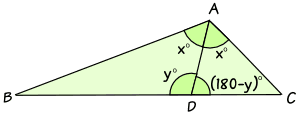
- 角BAD = 角DAC = x°
- 角ADB = y°
- 角ADC = (180 - y)°
在三角形 ABD上运用正弦定理:
sin x°/BD = sin y°/AB
所以 AB × sin x° = BD × sin y°
所以:
AB/BD = sin y°/sin x°
在三角形 ACD上运用正弦定理:
sin x°/DC = sin(180 - y)°/AC
所以 AC × sin x° = DC × sin(180 - y)°
所以 AC/DC = sin(180 - y)°/sin x°
因为 sin(180 - y)° = sin y°
所以:
AC/DC = sin y°/sin x°
把 AC/DC = sin y°/sin x° 与 AB/BD = sin y°/sin x° 拼合:
AC/DC = sin y°/sin x° = AB/BD
所以 AB/BD = AC/DC
如果三角形ABC 是等腰三角形,三角形ABD 和 ACD 便是 全等三角形,
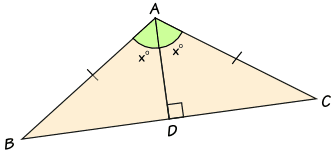
结果是一样的:
AB/BD = AC/DC
三、面积与相似
若相似三角形的边比例是 x:y,
则它们的面积比例是 x2:y2
例子:
这两个相似三角形的边比例是 2:1(一个三角形的边是另一个的两个倍):

那么它们的面积呢?
如果我们多画三条线,答案就浅而易见:
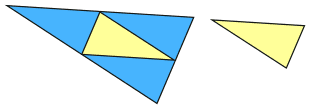
我们可以看到可以有四个小三角形放在大三角形里。
因此,如果长度是两倍,面积便是四倍
面积的比是 4:1
4:1 也可以写成 22:1
一般情况:
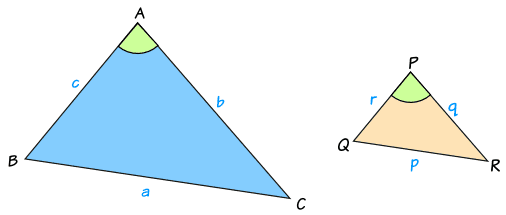
三角形ABC 和 PQR 是相似的,它们的边比例是 x:y
我们可以用求非直角三角形的面积页面里的公式来求面积
ABC 的面积 = ½bc sin A
PQR 的面积 = ½qr sin P
三角形长度的比是 x:y
q/b = y/x,所以 q = by/x
r/c = y/x,所以 r = cy/x
因为是相似三角形,所以角A 和 P 相等:
A = P
现在来计算:
| 三角形PQR 的面积: | ½qr sin P | |
| 代入 "q = by/x"、"r = cy/x"、"P=A": | ½(by/x)(cy/x) sin A | |
| 拼合 (by/x) 和 (cy/x): | ½(bycy/xx) sin A | |
| 简化: | ½(bcy2/x2) sin A | |
| 重排: | y2/x2 × ½(bc) sin A | |
| 就是: | y2/x2 × 三角形ABC 的面积 |
重排后得到的比例是:
三角形ABC 的面积:三角形PQR 的面积 = x2 : y2