反函数
反函数反过来做!
先看一个例子:
我们将函数 f(x) = 2x+3 写成流程图:
反函数就是把流程反过来:
所以: 2x+3 的反函数是: (y-3)/2
反函数通常是在函数名字后面加一个上标 "-1":
f-1(y)
我们说 "f y 的反函数"
所以 f(x) = 2x+3 的反函数是这样写:
f-1(y) = (y-3)/2
(我用 y,而不用 x,因为它们代表不同的值。)
还原
反函数把函数还原:
如果函数 f 把苹果变成香蕉,
反函数 f-1 把香蕉还原为苹果
例子:
用上面的公式,开始时 x=4:
f(4) = 2×4+3 = 11
然后把 11 代入反函数的公式里:
f-1(11) = (11-3)/2 = 4
得回原来的 4!
我们可以写成一行:
f-1( f(4) ) = 4
"f 反函数 的 f 的 4 等于 4"
所以把一个数值代入一个函数 f,然后把结果代入其反函数 f-1,就会得到原来的数值:
f-1( f(x) ) = x
把函数的次序倒转也是一样:
f( f-1(x) ) = x
例子:
开始:
f-1(11) = (11-3)/2 = 4
然后:
f(4) = 2×4+3 = 11
所以:
f( f-1(11) ) = 11
"f 的 f 反函数的 11 等于 11"
用代数来解
我们可以用代数来求反函数。用 "y" 代替 "f(x)",然后解 x:
| 函数: | f(x) | = | 2x+3 | |
| 用 "y" 代替 "f(x)": | y | = | 2x+3 | |
| 每边减 3: | y-3 | = | 2x | |
| 每边除 2: | (y-3)/2 | = | x | |
| 换边: | x | = | (y-3)/2 | |
| 结果 (用 "f-1(y)" 来代替 "x"): | f-1(y) | = | (y-3)/2 |
这是计算比较复杂的反函数的好方法。
把华氏转换为摄氏
一个好例子是华氏与摄氏相互转换:
| 将华氏转换为摄氏: | f(F) = (F - 32) × 59 | |
| 反函数(将摄氏转换为华氏)是: | f-1(C) = (C × 95) + 32 |
轮到你了:解反函数!
常见函数的反函数
上面的例子都很简单,因为我们都知道乘法的相反是除法,加法的相反是减法,但其他函数呢?
这是一个列表:
| 反函数 | 小心! | ||
| <=> | |||
| <=> | 不要除以零 | ||
| <=> | x 和 y 不能是零 | ||
| <=> | x 和 y ≥ 0 | ||
| <=> | n 不等于零 (n 为奇数、偶数、负数和正数都有不同的规则) |
||
| <=> | y > 0 | ||
| <=> | y 和 a > 0 | ||
| <=> | -π/2 to +π/2 | ||
| <=> | 0 to π | ||
| <=> | -π/2 to +π/2 | ||
(注意:去阅读反正弦、余弦和正切了解更多。)
小心!
留意 "小心!" 列,因为有些反函数只适用于某些数值。
例子:平方与平方根
取负数的平方,然后取反函数:
| 平方: | (-2)2 = 4 | |
| 反函数(平方根): | √(4) = 2 |
但我们得不到原来的数!结果是 2而不是 -2。我们不小心了!
平方函数(在现在情况下)没有反函数
但是,我们可以补救!
限制定义域(函数的输入)。
例子:(续)
不用负数作为输入。
就是说,把定义域限制为 x ≥ 0 就可以有反函数了。
所以:
- x2 没有反函数
- 但{x2 | x ≥ 0 }(这是合建构式符号,意思是 "x 平方,满足 x 大于或等于零这个性质")有反函数。
没有反函数?
我们来看这个图:
要有反函数,函数的值必然需要是唯一值。
如果一个 y值有两个或更多 x值,还原时应该选哪个呢?
| 一般函数 | 单射函数 | |
| 如果一个 y值有多于一个 x值,还原时应该选哪个呢? | 如果每个 x值的 y值是唯一的(没有其它 x值有这个 y值),从 y 还原到 x 就只有一个选择。 |
"每个 x值的 y值是唯一的" 这个概念有个名字,叫 "单射",也称 "一对一":
如果一个函数是"一对一"(单射)的,它就有反函数。
定义域与值域
我们为什么要 "限制定义域"?
|
简单地说,定义域是所有输入函数的值(值域的所有输出值)。 |
在现在情况下,上面的函数没有反函数,因为有些 y值有多于一个 x值。
| 但我们可以限制定义域,使得每个 y值只有一个唯一的 x值 …… | |
|
…… 这样函数就可以有反函数了:
注意:
|
…… 我们也可以……
我们可以把函数和反函数都写成 x 的函数 …… 反函数就写成 f-1(x),而不是 f-1(y):
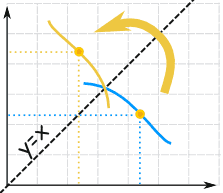
f(x) 和 f-1(x) 像彼此的镜像
(相对于对角线反转)。
换句话说:
f(x) 和 f-1(x) 的图是相对于直线 y=x 对称的
例子:平方和平方根(续)
我们首先把定义域限制为 x ≥ 0:
- {x2 | x ≥ 0 } "x 的平方,满足 x 大于或等于零的性质"
- {√x | x ≥ 0 } "x 的平方根,满足 x 大于或等于零的性质"
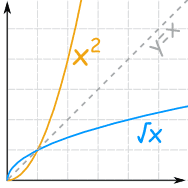
可以看到它们是彼此的"镜像",
相对于对角线 y=x.
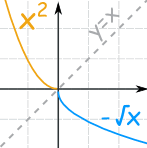
注意:把定义域限制为 x ≤ 0(小于或等于 0),反函数就是 f-1(x) = −√x:
- {x2 | x ≤ 0 }
- {−√x | x ≥ 0 }
也是反函数.
不一定有解的!
有时不可能解反函数。
例子:f(x) = x/2 + sin(x)
我们不能解反函数,因为我们不能解 "x":
y = x/2 + sin(x)
y …… ? = x
记法备注
我们这样写 f-1(x),但上标 "-1" 不是个指数(次方):
| f-1(x) | …… 和 …… | f(x)-1 是不同的 |
| 函数 f 的反函数 | f(x)-1 = 1/f(x)
(倒数) |
总括
- f(x) 的反函数是 f-1(y)
- 我们可以把 "流程图" 倒转来求反函数
- 或者用代数来解反函数:
- 用 "y" 来代替 "f(x)",然后
- 解 x
- 我们可能需要限制定义域才能使得函数有反函数