数列――找规律
若我们想找一个在数列里缺失的数,我们先要知道数列的规则
数列的定义
在数列和级数的网页中有详细的解释,但简单地说:
序列是一组顺序排列的东西,若这些东西是数,我们便称之为数列。
数列里的每一个数叫项(也叫 "元素"、"元" 或 "分子"):
找缺失的数
想找到缺失的数,要先找数列的规则。
有时候一眼便可以看到规律:
看到我们怎样用 "x" 和 "n" 来记下这个规则吗?
xn 的意思是 "第 n 项",所以地 3 项是写为 x3
在公式里,我们也用到 "n",所以第 3 项的公式是 32 = 9。这可以写成
x3 = 32 = 9
找到规则后,我们便可以用它来求任何一项。例如,要计算第 25 项的值,我们便把 25 "代入" 公式的n:
x25 = 252 = 625
再来一个例子:
例子:3,5,8,13,21、?
在 3 和 5 之后,所有的项都是前两下项的和:3 + 5 = 8、5 + 8 = 13 等等(这个数列是 斐波那契数列 的一部分):
规则:xn = xn-1 + xn-2
数列:3,5,8,13,21,34,55,89……
xn-1 是什么意思?意思是 "上一项",因为项数(n)少了1 (n-1)。
若 n 是 6,xn = x6 (第6项),xn-1 = x6-1 = x5 (第5项)
我们现在用数列的规则来求第6项:
x6 = x6-1 + x6-2
x6 = x5 + x4
我们已经知道第四项是 13,而五项是 21,所以第六项是:
x6 = 21 + 13 = 34
很简单……把数代入 "n" 里
很多规则
求数列中 "下一项" 的其中一个问题是我们可能找到不止一个合适的规则。
这数列的下一项是什么? 1,2,4,7,??
以下是三个答案(可能会有更多答案!):
答案 1:加 1、加 2,加 3、加 4……
这样:1+1=2、2+2=4、4+3=7, 7+4=11……
规则:xn = n(n-1)/2 + 1
数列:1,2,4,7,11,16,22……
(规则乍看相当复杂,但公式是对的)
答案 2:在 1 和 2 之后,把前两项相加,再加 1:
规则:xn = xn-1 + xn-2 + 1
数列:1,2,4,7,12,20,33……
答案 3:在 1、2 和 4 后,把前三项相加
规则:xn = xn-1 + xn-2 + xn-3
数列:1,2,4,7,13,24,44……
我们有三个合适的答案,但每个答案的数列是不同的(除了头四项之外).
哪个是对的?全部都对。
还有其他的答案…… |
……数列可能是每一个竞赛的第一名的号码……所以下一个数是……任何数! |
最简单的规则
当你有疑问时,选最简单而合理的规则,但也应该提及有其他答案。
计算差
有时候我们可以试试计算两个数的 差……这往往会揭示出数列背后的规律。
这是一个简单的例子:
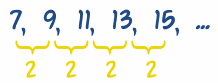
差永远是 2,所以答案里应该有 "2n" 这项。
试试 2n:
| n: | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 项 (xn): | 7 | 9 | 11 | 13 | 15 |
| 2n: | 2 | 4 | 6 | 8 | 10 |
| 误差: | 5 | 5 | 5 | 5 | 5 |
最后一行告诉我们答案永远少了 5,所以我们加 5 就行了:
规则:xn = 2n + 5在这个例子,我们随便试试就得到 "2n+5" 这个答案,但我们其实想要一个有规律的方法,给我们在解比较复杂的数列时应用。
二次差
在这数列: {1,2,4,7,11,16,22……} 我们需要求数与数之间的差……
……然后再求这些差之间的差(叫 二次差):
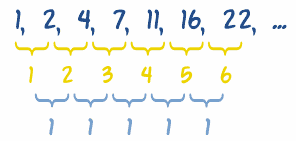
在这例子里,二次差 是 1。
用二次差时,我们乘以 "n2 / 2"。
在这例子,二次差是 1,所以我们试试 n2 / 2:
| n: | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 项 (xn): | 1 | 2 | 4 | 7 | 11 |
| n2: | 1 | 4 | 9 | 16 | 25 |
| n2 / 2: | 0.5 | 2 | 4.5 | 8 | 12.5 |
| 0.5 | 0 | -0.5 | -1 | -1.5 |
差不多,但误差好像以 0.5 逐项减少,所以我们可以试试这个:n2 / 2 - n/2
| n2 / 2 - n/2: | 0 | 1 | 3 | 6 | 10 |
|---|---|---|---|---|---|
| 误差: | 1 | 1 | 1 | 1 | 1 |
全部误差都是 1,加 1 就行了:
| n2 / 2 - n/2 + 1: | 1 | 2 | 4 | 7 | 11 |
|---|---|---|---|---|---|
| 误差: | 0 | 0 | 0 | 0 | 0 |
n2 / 2 - n/2 + 1 可以被简化为 n(n-1)/2 + 1
我们用 "試誤" 来找到一个合适的规则了:
规则:xn = n(n-1)/2 + 1
数列:1,2,4,7,11,16,22,29,37……
其他种类的数列
除了在 数列和级数这个网页里提到的数列:
之外,你也可以看看:
这世界有太多的数列了,不能尽录,但若你有一个数列,而且希望我把它放在这个网站,欢迎你告诉我。